题目内容
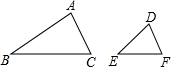如图，在△ABC和△DEF中，AB=2DE，AC=2DF，∠A=∠D，△ABC的面积是24，则△DEF的面积为（ ）A、2
| ||
| B、6 | ||
| C、12 | ||
| D、48 |
考点：相似三角形的判定与性质
专题：
分析：根据已知可证△ABC∽△DEF，且△ABC和△DEF的相似比为2，再根据相似三角形面积的比等于相似比的平方即可求△DEF的面积．
解答：解：因为在△ABC和△DEF中，AB=2DE，AC=2DF，
∴
=2，
又∵∠A=∠D，
∴△ABC∽△DEF，且△ABC和△DEF的相似比为2，
∵△ABC的面积是24，
∴△DEF的面积为24÷4=6．
故选B．
∴
| AB |
| DE |
又∵∠A=∠D，
∴△ABC∽△DEF，且△ABC和△DEF的相似比为2，
∵△ABC的面积是24，
∴△DEF的面积为24÷4=6．
故选B．
点评：本题考查相似三角形的判定和性质，相似三角形周长的比等于相似比，面积的比等于相似比的平方，难度中等．
练习册系列答案
阅读快车系列答案
相关题目
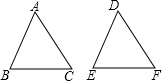如图，在△ABC与△DEF中，已有条件AB=DE，∠B=∠E，还需添加一个条件才能使△ABC≌△DEF，能添加的一个条件是（ ）| A、AC=DF |
| B、BC=DF |
| C、∠A=∠F |
| D、BC=EF |
如图，∠ACB=∠AED=90°，AC=BC，AD平分∠BAC交BC于点D，若AB=9，则△DEB的周长为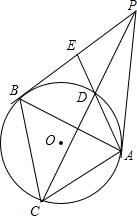
如图，点P是⊙O外的一点，PA，PB为⊙O的两条切线，E为PB的中点，连接EA，交⊙O于D点，连接PD并延长，交⊙O与C点．求证：AB=CD．
如图，已知∠C=90°，⊙O是Rt△ABC的内切圆，AB与⊙O相切于D，AO的延长线交BC于E．证明：AD•AE=AO•AC．