题目内容
有一块直角三角形的绿地,量得两直角边长分别为6m,8m,现在要将绿地扩充成等腰三角形,且扩充部分是以6m的直角边的反向延长线方向,求扩充后等腰三角形绿地的周长.
考点:勾股定理的应用
专题:分类讨论
分析:根据题意画出图形,分AB=AD,AB=BD,AD=BD三种情况进行讨论.
解答: 解:∵AC=8m,BC=6m,
解:∵AC=8m,BC=6m,
∴AB=
=10m.
当AB=AD时,如图1所示,
∵AC⊥BC,
∴BD=2BC=12m,
∴C△ABD=AB+AD+BD=10+10+12=22(m);
当AB=BD时,如图2所示,
∵AB=10m,BC=6m,
∴CD=10-6=4m,
∴AD=
=
=4
,
∴C△ABD=AB+AD+BD=10+4
+10=(20+4
)(m);
当AD=BD时,如图3所示,
设AD=x,则BC=x-BC=x-6,
在Rt△ADC中,
∵AC2+CD2=AD2,即82+(x-6)2=x2,解得x=
m,
∴C△ABD=AB+AD+BD=10+
+
=
(m).
综上所述,扩充后等腰三角形绿地的周长为22m,(20+4
)m,
m.
 解:∵AC=8m,BC=6m,
解:∵AC=8m,BC=6m,∴AB=
| 82+62 |
当AB=AD时,如图1所示,
∵AC⊥BC,
∴BD=2BC=12m,
∴C△ABD=AB+AD+BD=10+10+12=22(m);
当AB=BD时,如图2所示,
∵AB=10m,BC=6m,
∴CD=10-6=4m,
∴AD=
| AC2+CD2 |
| 82+42 |
| 5 |

∴C△ABD=AB+AD+BD=10+4
| 5 |
| 5 |
当AD=BD时,如图3所示,
设AD=x,则BC=x-BC=x-6,
在Rt△ADC中,
∵AC2+CD2=AD2,即82+(x-6)2=x2,解得x=
| 25 |
| 3 |
∴C△ABD=AB+AD+BD=10+
| 25 |
| 3 |
| 25 |
| 3 |
| 80 |
| 3 |
综上所述,扩充后等腰三角形绿地的周长为22m,(20+4
| 5 |
| 80 |
| 3 |
点评:本题考查的是勾股定理的应用,熟知在应用勾股定理解决实际问题时勾股定理与方程的结合是解决实际问题常用的方法,关键是从题中抽象出勾股定理这一数学模型,画出准确的示意图.领会数形结合的思想的应用是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
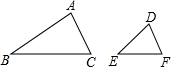 如图,在△ABC和△DEF中,AB=2DE,AC=2DF,∠A=∠D,△ABC的面积是24,则△DEF的面积为( )
如图,在△ABC和△DEF中,AB=2DE,AC=2DF,∠A=∠D,△ABC的面积是24,则△DEF的面积为( )A、2
| ||
| B、6 | ||
| C、12 | ||
| D、48 |
小明根据某个一次函数关系式填写了的表格:则空格中的数为( )
| x | -1 | 0 | 2 |
| y | -3 | 6 |
| A、16 | B、8 | C、12 | D、24 |
下列在正比例函数y=-4x的图象上的点是( )
| A、(1,4) |
| B、(-1,-4) |
| C、(4,-1) |
| D、(0.5,-2) |
下列变形正确的是( )
| A、由5=x-2得x=-5-2 | ||
B、由5y=0得y=
| ||
| C、由2x=3x+5得-5=3x-2x | ||
D、由3x=-2得x=-
|
已知∠A=65°,则∠A的补角等于( )
| A、95° | B、105° |
| C、115° | D、125° |
下列各式中,合并同类项错误的是( )
| A、x+x+x=x3 |
| B、3ab-3ab=0 |
| C、5a+2a=7a |
| D、4x2y-5x2y=-x2y |