Question

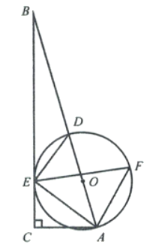
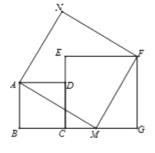
【题目】勾股定理历史悠久，三国时期的赵爽证明了勾股定理，后人借助“赵爽弦图”，用三个正方形证明勾股定理，如图所示，B，C，M，G在同一条直线上，四边形ABCD，四边形CEFG，四边形AMFN都为正方形，若五边形ABGFN的面积为34，CM=2，则△ABM的面积为( )

A.10B.C.5D.4

Answer 1

【答案】C

【解析】

可证得，设 ，则，根据五边形ABGFN的面积等于正方形AMFN的面积加上两个的面积即可求得结论．

∵四边形ABCD、四边形CEFG、四边形AMFN都为正方形，

∴∠ABM=∠AMF=∠MGF=90°，AM= MF，

∴∠AMB+∠BAM=90°，∠AMB+∠GMF=90°，

∴∠BAM=∠GMF，

∴，

设 ，则，

在中，

∴，即，

∵，即，

∴，

化简得：，

△ABM的面积为，

故选：C．