题目内容
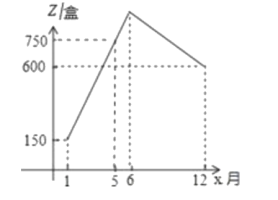
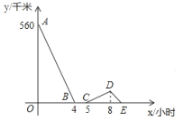
【题目】一辆慢车与一辆快车分别从甲、乙两地同时出发，匀速相向而行，两车在途中相遇后都停留一段时间，然后分别按原速一同驶往甲地后停车．设慢车行驶的时间为
小时，两车之间的距离为
千米，图中折线表示与之间的函数图象．当快车到达甲地时，慢车离甲地的距离为__________千米．
【答案】
【解析】
先根据题意得出慢车在甲地和相遇地之间往返分别用了
小时，慢车行驶小时的距离，快车
小时即可行驶完，利用两车速度之比进而求出快车速度和慢车速度；再求出快车到达甲地用时，即可求出快车到达甲地时慢车距甲地的距离．
解：∵根据题意可以得出：慢车和快车经过个小时后相遇，相遇后停留了
个小时，出发后两车之间的距离开始增大，快车到达甲地后两车之间的距离开始缩小，由图分析可知快车经过个小时后到达甲地，此段路程慢车需要行驶个小时，因此慢车和快车的速度之比为
∴设慢车速度为
，则快车的速度为
∴
∴
∴
，
∴快车的速度是
，慢车的速度是
∴快车和慢车相遇地离甲地的距离为
∴当慢车行驶了小时时，快车到达甲地，此时两车之间的距离，即慢车离甲地的距离为
．
故答案是：
练习册系列答案
相关题目
