题目内容
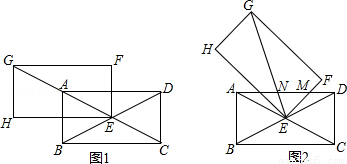
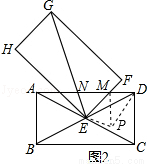
(10分)如图1,四边形ABCD、EFGH为全等的矩形.且矩形ABCD的对角线交于点E,点A在EG上,∠ACB=300.将矩形EFGH绕点E顺时针旋转а角(00<а<600),如图2,GE、FE与AD分别相交于N、M.
(1)求证:AN+DM>MN;
(2)若MN2+DM2=AN2,求旋转角а的大小.
(1)证明见试题解析;(2)45°.
【解析】
试题分析:(1)根据矩形的对角线互相平分且相等可得AE=DE,再求出∠AED=120°,将△AEN绕点E顺时针旋转120°得到△DPE,连接MP,根据旋转的性质可得EP=NE,DP=AN,∠DEP=∠EN,再求出∠MEN=∠MEP=60°,然后利用“边角边”证明△MEN和△MEP全等,根据全等三角形对应边相等可得MN=MP,然后利用三角形的任意两边之和大于第三边证明即可;
(2)利用勾股定理逆定理判断出△DPM是直角三角形,根据全等三角形对应角相等可得∠EMN=∠EMP=45°,利用三角形的内角和定理求出∠MNE=75°,再根据三角形的一个外角等于与它不相邻的两个内角的和求出∠AEN=45°,即为旋转角度数.
试题解析:(1)∵四边形ABCD是矩形,∴AE=DE,
∵∠ACB=30°,∴∠AED=180°﹣30°×2=120°,
将△AEN绕点E顺时针旋转120°得到△DPE,连接MP,
则EP=NE,DP=AN,∠DEP=∠EN,
∵∠AED=120°,∴∠MEN=∠MEP=60°,
在△MEN和△MEP中,
∵EP=NE,∠MEN=∠MEP,EM=EM,∴△MEN≌△MEP(SAS),∴MN=MP,
由三角形的三边关系得,DP+DM>MP,∴AN+DM>MN;
(2)【解析】
∵MN2+DM2=AN2,∴△DPM是直角三角形,∠DMP=90°,
∵△MEN≌△MEP,∴∠EMN=∠EMP=45°,
在△MNE中,∠MNE=180°﹣45°﹣60°=75°,
在△ANE中,∠AEN=∠MNE﹣∠CAD=75°﹣30°=45°,
∴旋转角为45°.
考点:旋转的性质.
考点分析: 考点1:图形的平移与旋转 定义:将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移。平移是图形变换的一种基本形式。平移不改变图形的形状和大小,平移可以不是水平的。 平移基本性质:
经过平移,对应线段平行(或共线)且相等,对应角相等,对应点所连接的线段平行且相等;
平移变换不改变图形的形状、大小和方向(平移前后的两个图形是全等形)。
(1)图形平移前后的形状和大小没有变化,只是位置发生变化;
(2)图形平移后,对应点连成的线段平行(或在同一直线上)且相等
(3)多次连续平移相当于一次平移。
(4)偶数次对称后的图形等于平移后的图形。
(5)平移是由方向和距离决定的。
这种将图形上的所有点都按照某个方向作相同距离的位置移动,叫做图形的平移运动,简称为平移
平移的条件:确定一个平移运动的条件是平移的方向和距离。 平移的三个要点
1 原来的图形的形状和大小和平移后的图形是全等的。
2 平移的方向。(东南西北,上下左右,东偏南n度,东偏北n度,西偏南n度,西偏北n度)
3 平移的距离。(长度,如7厘米,8毫米等) 平移作用:
1.通过简单的平移可以构造精美的图形。也就是花边,通常用于装饰,过程就是复制-平移-粘贴。
2.平移长于平行线有关,平移可以将一个角,一条线段,一个图形平移到另一个位置,是分散的条件集中到一个图形上,使问题得到解决。 平移作图的步骤:
(1)找出能表示图形的关键点;
(2)确定平移的方向和距离;
(3)按平移的方向和距离确定关键点平移后的对应点;
(4)按原图的顺序,连结各对应点。 试题属性
- 题型:
- 难度:
- 考核:
- 年级:

(10分)张明、王成两位同学初二一学年10次数学单元自我检测的成绩(成绩均为整数,且个位数为0)分别如下图所示:利用图中提供的信息,解答下列问题.
(1)完成下表
姓名 | 平均成绩 | 中位数 | 众数 | 方差(S2) |
张明 | 80 | 80 | ||
王成 | 260 |
(2)如果将90分以上(含90分)的成绩视为A等,则获得成绩为A等多的同学是 ;
(3)根据图表信息,请你对这位两同学各提一条不超过20个字的学习建议,并说明提出建议的原因.

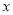 的一元二次方程
的一元二次方程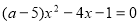 有实数根,则
有实数根,则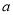 满足条件是( )
满足条件是( )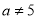 B、
B、 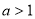 且
且 C、.
C、. 且
且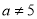 D、
D、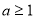
 的平方根是( ).
的平方根是( ). B.12 C
B.12 C D.
D.
 的两个实数根,求:
的两个实数根,求: 的值.
的值. 的解为 .
的解为 .
