题目内容
9.若点A(1,2),B(-2,-3)在直线y=kx+b上,则函数y=$\frac{k}{x}$的图象在( )| A. | 第一、三象限 | B. | 第一、二象限 | C. | 第二、四象限 | D. | 第二、三象限 |
分析 由点A、B的坐标利用待定系数法可求出一次函数解析式,再根据k>0即可得出反比例函数y=$\frac{k}{x}$的图象所在的象限.
解答 解:∵点A(1,2),B(-2,-3)在直线y=kx+b上,
∴$\left\{\begin{array}{l}{k+b=2}\\{-2k+b=-3}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=\frac{5}{3}}\\{b=\frac{1}{3}}\end{array}\right.$,
∴函数y=$\frac{\frac{5}{3}}{x}$的图象在第一、三象限.
故选A.
点评 本题考查了反比例函数的图象以及待定系数法求一次函数解析式,根据点A、B的坐标利于待定系数法可求出一次函数解析式是解题的关键.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
9.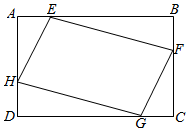 如图,矩形ABCD中,AB=10,BC=5,点E,F,G,H分别在矩形ABCD各边上,且AE=CG,BF=DH,则四边形EFGH周长的最小值为( )
如图,矩形ABCD中,AB=10,BC=5,点E,F,G,H分别在矩形ABCD各边上,且AE=CG,BF=DH,则四边形EFGH周长的最小值为( )
 如图,矩形ABCD中,AB=10,BC=5,点E,F,G,H分别在矩形ABCD各边上,且AE=CG,BF=DH,则四边形EFGH周长的最小值为( )
如图,矩形ABCD中,AB=10,BC=5,点E,F,G,H分别在矩形ABCD各边上,且AE=CG,BF=DH,则四边形EFGH周长的最小值为( )| A. | 5$\sqrt{5}$ | B. | 10$\sqrt{5}$ | C. | 10$\sqrt{3}$ | D. | 15$\sqrt{3}$ |
4.下列函数中,满足y的值随x的值增大而增大的是( )
| A. | y=3x-1 | B. | y=-2x | C. | y=$\frac{1}{x}$ | D. | y=x2 |
1.下列调查方式中,适合用普查方式的是( )
| A. | 要了解一批等灯泡的使用寿命 | |
| B. | 要了解栾城电视台“栾城新闻”的收视率 | |
| C. | 要了解某校篮球队12名队员的身高状况 | |
| D. | 要了解全国人民对“春节连欢晚会”的满意度 |
 如图,∠AOB=90°,OE是∠AOB的平分线,OD是∠BOC的平分线,若∠EOD=70°,则∠BOC的度数是50°.
如图,∠AOB=90°,OE是∠AOB的平分线,OD是∠BOC的平分线,若∠EOD=70°,则∠BOC的度数是50°.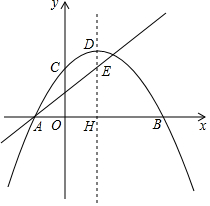 已知:如图,抛物线y=-$\frac{1}{4}$(x-h)2+k与x轴交于A、B,与y轴交于C,抛物线的顶点为D,对称轴交x轴于H,直线y=$\frac{3}{4}$x+$\frac{3}{2}$经过点A与对称轴交于E,点E的纵坐标为3.
已知:如图,抛物线y=-$\frac{1}{4}$(x-h)2+k与x轴交于A、B,与y轴交于C,抛物线的顶点为D,对称轴交x轴于H,直线y=$\frac{3}{4}$x+$\frac{3}{2}$经过点A与对称轴交于E,点E的纵坐标为3.



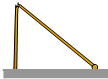 如图,一旗杆被大风刮断,旗杆的顶部着地点到旗杆底部的距离为4m,折断点离旗杆底部的高度为3m,则旗杆的高度为8m.
如图,一旗杆被大风刮断,旗杆的顶部着地点到旗杆底部的距离为4m,折断点离旗杆底部的高度为3m,则旗杆的高度为8m. 如图,直线a∥b,射线DF与直线a相交于点C,过点D作DE⊥b于点E,已知∠1=30°,求∠2的度数.
如图,直线a∥b,射线DF与直线a相交于点C,过点D作DE⊥b于点E,已知∠1=30°,求∠2的度数.