题目内容
2.如果将抛物线y=x2+2x-1向上平移,使它经过点A(0,3),那么所得新抛物线的表达式是y=x2+2x+3.分析 设平移后的抛物线解析式为y=x2+2x-1+b,把点A的坐标代入进行求值即可得到b的值.
解答 解:设平移后的抛物线解析式为y=x2+2x-1+b,
把A(0,3)代入,得
3=-1+b,
解得b=4,
则该函数解析式为y=x2+2x+3.
故答案是:y=x2+2x+3.
点评 主要考查了函数图象的平移,要求熟练掌握平移的规律:左加右减,上加下减.并用规律求函数解析式.会利用方程求抛物线与坐标轴的交点.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
13.设二次函数y=(x-3)2-4图象的对称轴为直线l,若点M在直线l上,则点M的坐标可能是( )
| A. | (1,0) | B. | (3,0) | C. | (-3,0) | D. | (0,-4) |
14.关于x的一元二次方程kx2+2x+1=0有两个不相等的实数根,则k的取值范围是( )
| A. | k>-1 | B. | k≥-1 | C. | k≠0 | D. | k<1且k≠0 |
12.圆内接四边形ABCD中,已知∠A=70°,则∠C=( )
| A. | 20° | B. | 30° | C. | 70° | D. | 110° |
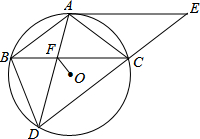 如图,△ABC内接于⊙O,AB=AC,BD为⊙O的弦,且AB∥CD,过点A作⊙O的切线AE与DC的延长线交于点E,AD与BC交于点F.
如图,△ABC内接于⊙O,AB=AC,BD为⊙O的弦,且AB∥CD,过点A作⊙O的切线AE与DC的延长线交于点E,AD与BC交于点F.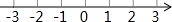 解不等式组:$\left\{\begin{array}{l}{4x>2x-6}\\{\frac{x-1}{3}≤\frac{x+1}{9}}\end{array}\right.$,并把解集在数轴上表示出来.
解不等式组:$\left\{\begin{array}{l}{4x>2x-6}\\{\frac{x-1}{3}≤\frac{x+1}{9}}\end{array}\right.$,并把解集在数轴上表示出来.