题目内容
1.平面上边长为1的正方形ABCD绕着其中心旋转45°得到正方形A′B′C′D′,那么这两个正方形重叠部分的面积为2$\sqrt{2}-2$.分析 先根据题意画出图形,从而得到重叠部分的面积等=正方形的面积-4个等腰直角三角形的面积.
解答 解:如图所示:
设AE=AF=x,则EF=$\sqrt{2}x$.
根据题意可知:AE=EL+LD=1,即2x+$\sqrt{2}x$=1.
解得:x=$\frac{2-\sqrt{2}}{2}$.
∴AE=$\frac{2-\sqrt{2}}{2}$.
∴△AEF的面积=$\frac{1}{2}×AE×AF=\frac{1}{2}×(\frac{2-\sqrt{2}}{2})^{2}$.
∴重合部分的面积=正方形的面积-4×△AEF的面积=1-4×$\frac{1}{2}×(\frac{2-\sqrt{2}}{2})^{2}$=2$\sqrt{2}-2$.
故答案为:2$\sqrt{2}-2$.
点评 本题主要考查的是旋转的性质,根据题意画出图形,明确重合部分的面积=正方形的面积-4×△AEF的面积是解题的关键.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
15.A、B两地相距30千米,甲从A地出发以每小时5千米的速度向目的地B行走,则甲与B地间的距离s(千米)与甲行走的时间t(小时)间的函数关系是( )
| A. | s=5t(t≥0) | B. | s=5t(0≤t≤6) | C. | s=30+5t(0≤t≤6) | D. | s=30-5t(0≤t≤6) |
10.下列图案中,既是中心对称图形,又是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
 如图,已知AD是△BAC的角平分线,AD的垂直平分线EF交BC的延长线于点E,试说明:ED2=EC•EB.
如图,已知AD是△BAC的角平分线,AD的垂直平分线EF交BC的延长线于点E,试说明:ED2=EC•EB.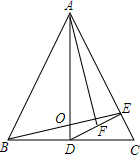 如图,在等腰△ABC中,AB=AC,AD⊥BC,垂足为D,DE⊥AC,垂足为E,且DF=EF,求证:AF⊥BE.
如图,在等腰△ABC中,AB=AC,AD⊥BC,垂足为D,DE⊥AC,垂足为E,且DF=EF,求证:AF⊥BE.