题目内容
18.某同学在计算3(4+1)(42+1)时,把3写成(4-1)后,发现可以连续运用两数和乘以这两数差公式计算:3(4+1)(42+1)=(4-1)(4+1)(42+1)=(42-1)(42+1)=162-1.
(1)请借鉴该同学的经验,计算:(1+$\frac{1}{2}$)(1+$\frac{1}{{2}^{2}}$)(1+$\frac{1}{{2}^{4}}$)(1+$\frac{1}{{2}^{8}}$)+$\frac{1}{{2}^{15}}$=2;
(2)请逆用平方差公式计算:(1-$\frac{1}{{2}^{2}}$)(1-$\frac{1}{{3}^{2}}$)(1-$\frac{1}{{4}^{2}}$)…(1-$\frac{1}{1{0}^{2}}$)
分析 (1)把原式前面乘2×(1-$\frac{1}{2}$),进一步利用平方差公式计算即可;
(2)利用平方差公式分解,进一步计算约分得出答案即可.
解答 解:(1)原式=2×(1-$\frac{1}{2}$)(1+$\frac{1}{2}$)(1+$\frac{1}{{2}^{2}}$)(1+$\frac{1}{{2}^{4}}$)(1+$\frac{1}{{2}^{8}}$)+$\frac{1}{{2}^{15}}$
=2×(1-$\frac{1}{{2}^{2}}$)(1+$\frac{1}{{2}^{2}}$)(1+$\frac{1}{{2}^{4}}$)(1+$\frac{1}{{2}^{8}}$)+$\frac{1}{{2}^{15}}$
=2×(1-$\frac{1}{{2}^{4}}$)(1+$\frac{1}{{2}^{4}}$)(1+$\frac{1}{{2}^{8}}$)+$\frac{1}{{2}^{15}}$
=2×(1-$\frac{1}{{2}^{8}}$)(1+$\frac{1}{{2}^{8}}$)+$\frac{1}{{2}^{15}}$
=2×(1-$\frac{1}{{2}^{16}}$)+$\frac{1}{{2}^{15}}$
=2-$\frac{1}{{2}^{15}}$+$\frac{1}{{2}^{15}}$
=2.
(2)原式=(1-$\frac{1}{2}$)(1+$\frac{1}{2}$)(1-$\frac{1}{3}$)(1+$\frac{1}{3}$)(1-$\frac{1}{4}$)(1+$\frac{1}{4}$)…(1-$\frac{1}{10}$)(1+$\frac{1}{10}$)
=$\frac{1}{2}$×$\frac{3}{2}$×$\frac{2}{3}$×$\frac{4}{3}$×$\frac{3}{4}$×$\frac{5}{4}$×…×$\frac{9}{10}$×$\frac{11}{10}$
=$\frac{1}{2}$×$\frac{11}{10}$
=$\frac{11}{20}$.
点评 此题考查平方差公式,掌握平方差公式的灵活运用是解决问题的关键.

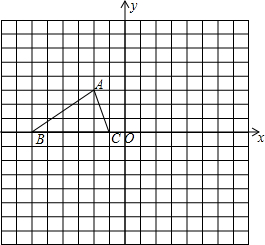 如图,已知△ABC的三个顶点的坐标分别为A(-2,3)、B(-6,0)、C(-1,0).
如图,已知△ABC的三个顶点的坐标分别为A(-2,3)、B(-6,0)、C(-1,0).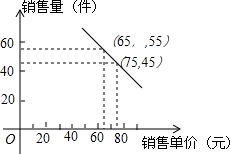 超市市场部整理出销售某品牌新款童装的销售量与销售单价的相关信息如下:
超市市场部整理出销售某品牌新款童装的销售量与销售单价的相关信息如下: