Question

3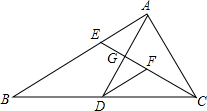．如图，在△ABC中，AD是BC边上的中线，点E在边AB上，CE与AD交于点G，点F是CE的中点，点G是EF的中点．求证：AE=$\frac{1}{2}$BE．

Answer 1

分析 由三角形中位线定理推知DF=$\frac{1}{2}$BE．由全等三角形的判定定理ASA得到△AEG≌△DFG，则其对应边相等：AE=DF，根据等量代换得到结论．

解答 证明：∵AD是BC边上的中线，点F是CE的中点，
∴DF是△BCF的中位线，
∴DF=$\frac{1}{2}$BE，DF∥AB，
∴∠AEG=∠DFG．
又∵点G是EF的中点，
∴EG=FG．
在△AEG与△DFG中，
$\left\{\begin{array}{l}{∠AEG=}\\{EG=FG}\\{∠EGA=∠FGD}\end{array}\right.$，
∴△AEG≌△DFG（ASA），
∴AE=DF，
∴AE=$\frac{1}{2}$BE．

点评 本题考查了全等三角形的判定与性质和三角形中位线定理．在应用全等三角形的判定时，要注意三角形间的公共边、公共角以及对顶角，必要时添加适当辅助线构造三角形．