题目内容
已知关于x的二次函数的图象的顶点坐标为(-1,2),且图象过点(1,-3),求这个二次函数的表达式和它的图象与坐标轴的交点坐标.
考点:待定系数法求二次函数解析式,二次函数的性质
专题:计算题
分析:由于已知顶点坐标,则可设顶点式y=a(x+1)2+2,再把(1,-3)代入求出a的值即可得到二次函数的表达式;然后计算出自变量为0时所对应的函数值和自变量为0时所对应的函数值,则可得到抛物线与坐标轴的交点坐标.
解答:解:设抛物线解析式为y=a(x+1)2+2,
把(1,-3)代入得a•(1+1)2+2=-3,解得a=-
,
所以二次函数解析式为y=-
(x+1)2+2,
当y=0时,-
(x+1)2+2,解得x1=-1+
,x2=-1-
,所以抛物线与x轴的交点坐标为(-1+
,0)、(-1-
,0);
当x=0时,y=-
+2=
,所以抛物线与y轴的交点坐标为(0,
).
把(1,-3)代入得a•(1+1)2+2=-3,解得a=-
| 5 |
| 4 |
所以二次函数解析式为y=-
| 5 |
| 4 |
当y=0时,-
| 5 |
| 4 |
2
| ||
| 5 |
2
| ||
| 5 |
2
| ||
| 5 |
2
| ||
| 5 |
当x=0时,y=-
| 5 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
点评:本题考查了待定系数法求二次函数的解析式:在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解;当已知抛物线与x轴有两个交点时,可选择设其解析式为交点式来求解.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
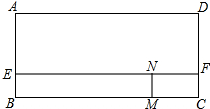 如图,已知矩形ABCD,AB=6cm,BC=8cm,E、F分别是AB、CD上的点,且AE=DF=4cm,两动点M、N分别从C、F两点同时出发沿CB、FE均以2cm/s的速度向B、E两点运动,猜测当M、N运动多长时间,矩形CFNM与矩形AEFD相似?写出你的猜测过程,与同学交流.
如图,已知矩形ABCD,AB=6cm,BC=8cm,E、F分别是AB、CD上的点,且AE=DF=4cm,两动点M、N分别从C、F两点同时出发沿CB、FE均以2cm/s的速度向B、E两点运动,猜测当M、N运动多长时间,矩形CFNM与矩形AEFD相似?写出你的猜测过程,与同学交流. 已知CE∥DF,∠ABF=100°,∠CAB=20°,则∠ACE的度数为多少度?
已知CE∥DF,∠ABF=100°,∠CAB=20°,则∠ACE的度数为多少度? 某市自1月1日起对市区民用管道天然气价格进行调整,实行阶梯式气价,调整后的收费价格如表所示:
某市自1月1日起对市区民用管道天然气价格进行调整,实行阶梯式气价,调整后的收费价格如表所示: