题目内容
18.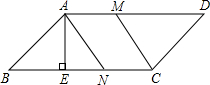 如图,平行四边形ABCD中,AD=9cm,CD=3$\sqrt{2}$cm,∠B=45°,点M、N分别以A、C为起点,1cm/秒的速度沿AD、CB边运动,设点M、N运动的时间为t秒(0≤t≤6)
如图,平行四边形ABCD中,AD=9cm,CD=3$\sqrt{2}$cm,∠B=45°,点M、N分别以A、C为起点,1cm/秒的速度沿AD、CB边运动,设点M、N运动的时间为t秒(0≤t≤6)(1)求BC边上高AE的长度;
(2)连接AN、CM,当t为何值时,四边形AMCN为菱形;
(3)作MP⊥BC于P,NQ⊥AD于Q,当t为何值时,四边形MPNQ为正方形.
分析 (1)先由平行四边形的性质得出AB=CD=3$\sqrt{2}$cm.再解直角△ABE,即可求出AE的长度;
(2)先证明四边形AMCN为平行四边形,则当AN=AM时,四边形AMCN为菱形.根据AN=AM列出方程32+(6-t)2=t2,解方程即可;
(3)先证明四边形MPNQ为矩形,则当QM=QN时,四边形MPNQ为正方形.根据QM=QN列出方程2t-6=3,解方程即可.
解答 解:(1)∵四边形ABCD是平行四边形,
∴AB=CD=3$\sqrt{2}$cm.
在直角△ABE中,∵∠AEB=90°,∠B=45°,
∴AE=AB•sin∠B=3$\sqrt{2}$×$\frac{\sqrt{2}}{2}$=3(cm);
(2)∵点M、N分别以A、C为起点,1cm/秒的速度沿AD、CB边运动,设点M、N运动的时间为t秒(0≤t≤6),
∴AM=CN=t,
∵AM∥CN,
∴四边形AMCN为平行四边形,
∴当AN=AM时,四边形AMCN为菱形.
∵BE=AE=3,EN=6-t,
∴AN2=32+(6-t)2,
∴32+(6-t)2=t2,
解得t=$\frac{15}{4}$.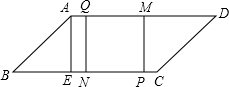 故当t为$\frac{15}{4}$时,四边形AMCN为菱形;
故当t为$\frac{15}{4}$时,四边形AMCN为菱形;
(3)∵MP⊥BC于P,NQ⊥AD于Q,QM∥NP,
∴四边形MPNQ为矩形,
∴当QM=QN时,四边形MPNQ为正方形.
∵AM=CN=t,BE=3,
∴AQ=EN=BC-BE-CN=9-3-t=6-t,
∴QM=AM-AQ=t-(6-t)=2t-6,
∵QN=AE=3,
∴2t-6=3,
解得t=4.5.
故当t为4.5时,四边形MPNQ为正方形.
点评 本题考查了平行四边形的性质,解直角三角形,菱形的判定,正方形的判定,利用数形结合与方程思想是解题的关键.

| A. | 随k值的变化而变化 | B. | 有两个不相等的实数根 | ||
| C. | 有两个实数根 | D. | 无实数根 |
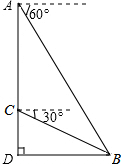 青青草原上,灰太狼每天都想着如何抓羊,而且是屡败屡试,永不言弃.(如图所示)一天,灰太狼在自家城堡顶部A处测得懒羊羊所在地B处的俯角为60°,然后下到城堡的C处,测得B处的俯角为30°.已知AC=50米,这时懒羊羊距离堡底部D有多远?
青青草原上,灰太狼每天都想着如何抓羊,而且是屡败屡试,永不言弃.(如图所示)一天,灰太狼在自家城堡顶部A处测得懒羊羊所在地B处的俯角为60°,然后下到城堡的C处,测得B处的俯角为30°.已知AC=50米,这时懒羊羊距离堡底部D有多远?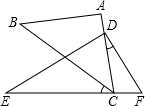 将一副直角三角板如图摆放,点C在EF上,AC经过点D,∠A=∠EDF=90°,∠BCE=40°,则∠CDF=25°.
将一副直角三角板如图摆放,点C在EF上,AC经过点D,∠A=∠EDF=90°,∠BCE=40°,则∠CDF=25°.