题目内容
6.已知线段AB.(1)M是线段AB上一点,且此时所有线段之和为20,求线段AB的长;
(2)直线AB上有一点C,且BC=4,N是AC的中点,求AN的长.
分析 (1)先根据题意画出图形,由AM+MB=AB得到2AB=20,从而可求得AB的长;
(2)分为点C在AB上和点C在AB的延长线上两种情况计算即可.
解答 解:(1)如图1所示:
根据题意可知:AM+MB+AB=20.
∵AM+MB=AB,
∴2AB=20.
∴AB=10.
(2)如图2所示:点C在AB的延长线上.
∵AB=10,BC=4,
∴AC=AB+BC=10+4=14.
∵N是AC的中点,
∴AN=$\frac{1}{2}AC$=$\frac{1}{2}×14$=7.
如图3所示;点C在AB上.
∵AB=10,BC=4,
∴AC=10-4=6.
∵N是AC的中点,
∴AN=$\frac{1}{2}AC$=$\frac{1}{2}×6$=3.
∴AN的长为3或7.
点评 本题主要考查的是两点间的距离,分类讨论是解题的关键.

练习册系列答案
相关题目
18.计算(-1)2016结果正确的是( )
| A. | -1 | B. | 1 | C. | -2016 | D. | 2016 |
16.抛物线y=$\frac{1}{2}$x2的图象向左平移2个单位,再向下平移1个单位,则所得抛物线的解析式为( )
| A. | y=$\frac{1}{2}$(x-2)2+1 | B. | y=$\frac{1}{2}$(x-2)2-1 | C. | y=$\frac{1}{2}$(x+2)2+1 | D. | y=$\frac{1}{2}$(x+2)2-1 |
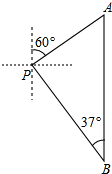 如图,小明从P处出发,沿北偏东60°方向行驶200米到达A处,接着向正南方向行驶一段时间到达B处.在B处观测到出发时所在的P处在北偏西37°方向上,这时P、B两点相距多少米?(精确到1米,参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,
如图,小明从P处出发,沿北偏东60°方向行驶200米到达A处,接着向正南方向行驶一段时间到达B处.在B处观测到出发时所在的P处在北偏西37°方向上,这时P、B两点相距多少米?(精确到1米,参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,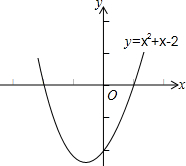 观察函数的图象.完成填空;
观察函数的图象.完成填空;