题目内容
(本题12分)在△ABC中,AB=AC,D是直线BC上一点(不与点B、C重合),以AD为一边在AD的右侧作△ADE,AD=AE,∠DAE=∠BAC,连接CE.
(1)如图1,当点D在线段BC上时,求证:△ABD≌△ACE.
(2)设∠BAC=α,∠BCE=β.
①如图1,当点D在线段BC上时,则α,β之间有怎样的数量关系?写出证明过程;
②当点D在直线BC上时,则α,β之间有怎样的数量关系?请画出图形并直接写出你的结论.


(1)详见解析;(2)①α+β=180°;α=β
【解析】
试题分析:(1)证明:∵∠BAC=∠DAE,
∴∠BAD=∠CAE,
∵在△ABD和△ACE中,

∴△ABD≌△ACE(SAS);
(2)①α+β=180°,
理由:∵∠BAC=∠DAE,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC.
即∠BAD=∠CAE.
在△ABD与△ACE中,
∴△ABD≌△ACE,
∴∠B=∠ACE.
∴∠B+∠ACB=∠ACE+∠ACB.
∴∠B+∠ACB=β,
∴α+∠B+∠ACB=180°,
∴α+β=180°
②当点D在射线BC上时,α+β=180°;
当点D在射线BC的反向延长线上时,α=β
考点:三角形的全等

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
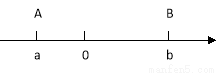
 和
和 的两点之间的距离表示为__ ________.(3分)
的两点之间的距离表示为__ ________.(3分) ,化简:
,化简: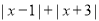 (4分)
(4分) ,则
,则 是 ( )
是 ( ) 

 千克,如果这箱草莓重4.98千克,那么这箱草莓质量 标准.(填“符合”或“不符合”)
千克,如果这箱草莓重4.98千克,那么这箱草莓质量 标准.(填“符合”或“不符合”)