题目内容
数学实验室:(本题12分)
点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a-b|.
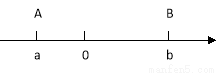
利用数形结合思想回答下列问题:
①数轴上表示2和5两点之间的距离是________,数轴上表示1和﹣3的两点之间的距离是________.(2分)
②数轴上表示 和
和 的两点之间的距离表示为__ ________.(3分)
的两点之间的距离表示为__ ________.(3分)
③若 表示一个有理数,且
表示一个有理数,且 ,化简:
,化简: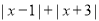 (4分)
(4分)
④若 表示一个有理数,且
表示一个有理数,且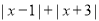 >4,则有理数
>4,则有理数 的取值范围是___________________(3分)
的取值范围是___________________(3分)
(1)3;4;(2)|x+2|;(3)4;(5)x>1或x<﹣3
【解析】
试题分析:①根据两点间距离公式求解即可;
②根据已知给出的求两点间距离的公式表示即可;
③根据x的取值范围,分别判断x﹣1与x+3的正负,然后根据绝对值的性质求解即可;
④根据已知的不等式进行分析,从而不难求得有理数x的取值范围.
试题解析:①∵2和5两点之间的距离是:|2﹣5|=3,1和﹣3的两点之间的距离是:|1﹣(﹣3)|=4,
∴数轴上表示2和5两点之间的距离是:3,数轴上表示1和﹣3的两点之间的距离是:4.
②∵x和﹣2的两点之间的距离为:|x﹣(﹣2)|=|x+2|,
∴数轴上表示x和﹣2的两点之间的距离表示为:|x+2|.
③∵﹣3<x<1,
∴|x﹣1|+|x+3|=1﹣x+x+3=4.
④当x>1时,原式=x﹣1+x+3=2x+2>4,解得,x>1;
当x<﹣3时,原式=﹣x+1﹣x﹣3=﹣2x﹣2>4,解得,x<﹣3;
当﹣3<x<1时,原式=﹣x+1+x+3=4,不符合题意,故舍去;
∴有理数x的取值范围是:x>1或x<﹣3.
考点:1.绝对值;22.数轴;3.代数式求值;4.解一元一次不等式.

 名校课堂系列答案
名校课堂系列答案

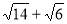 >
>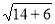 的推理过程:
的推理过程: ,
,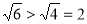 ,所以
,所以 , 又
, 又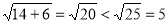 ,所以
,所以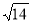 、
、 ,利用勾股定理得斜边长的平方为
,利用勾股定理得斜边长的平方为 ,因为斜边长大于0,故斜边长为
,因为斜边长大于0,故斜边长为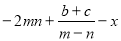 的值.
的值. 的所有数乘积为 .
的所有数乘积为 .

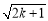 x+1=0有两个不相等的实数根,那么k的取值范围是
x+1=0有两个不相等的实数根,那么k的取值范围是 B.k<
B.k<