题目内容
小王投资10万元购买花卉和树苗.已知:
①花卉的利润y(万元)与投资金额x(万元)的函数关系式是:y=-2x+3.
②树苗的利润y(万元)与投资金额x(万元)的函数关系式是:y=3x-5.
问:投资花卉的金额不多于投资树苗的金额,不少于投资金额的
,求小王最多获利多少万元?最少获利多少万元?
①花卉的利润y(万元)与投资金额x(万元)的函数关系式是:y=-2x+3.
②树苗的利润y(万元)与投资金额x(万元)的函数关系式是:y=3x-5.
问:投资花卉的金额不多于投资树苗的金额,不少于投资金额的
| 1 |
| 4 |
考点:一次函数的应用
专题:
分析:设小王投资花卉x万元,则投资树苗(10-x)万元,投资花卉的利润是(-2x+3)万元,投资树苗的利润是3(10-x)-5=25-3x万元,则投资的获利即可表示成x的函数,然后求得x的范围,依据一次函数的性质求解.
解答:解:设小王投资花卉x万元,则投资树苗(10-x)万元,投资花卉的利润是(-2x+3)万元,投资树苗的利润是3(10-x)-5=25-3x万元.
根据题意得:
,
解得:2.5≤x≤5,
获利w=(-2x+3)+(25-3x)=28-5x,
则当x=2.5时,w取得最大值,是28-5×2.5=15.5(万元).
根据题意得:
|
解得:2.5≤x≤5,
获利w=(-2x+3)+(25-3x)=28-5x,
则当x=2.5时,w取得最大值,是28-5×2.5=15.5(万元).
点评:本题考查了一次函数的应用,正确理解函数的定义,利用x表示出投资树苗的利润是关键.

练习册系列答案
相关题目
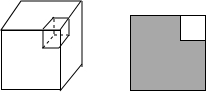 如图所示,在边长为a的正方形中减去一个边长为b的小正方形(a>b),剩下的部分的面积,可得到平方差公式;那么在边长a的正方体中减去一个边长为b的小正方体(a>b),剩下的部分的体积为a3-b3,它等于( )
如图所示,在边长为a的正方形中减去一个边长为b的小正方形(a>b),剩下的部分的面积,可得到平方差公式;那么在边长a的正方体中减去一个边长为b的小正方体(a>b),剩下的部分的体积为a3-b3,它等于( )| A、(a+b)(a2-ab+b2) |
| B、(a-b)(a2+ab+b2) |
| C、(a-b)(a2+b2) |
| D、(a+b)(a2-b2) |
下列调查中,适宜采用全面调查(普查)的是( )
| A、对全国中学生心理健康现状的调查 |
| B、对冷饮市场上冰淇淋质量情况的调查 |
| C、对西安市市民实施低碳生活情况的调查 |
| D、对“神舟九号”飞船零部件状况的检查 |
 如图,在三角形纸片ABC中,∠C=90°,AC=6,折叠该纸片使点C落在AB边上的D点处,折痕BE与AC交于点E.若AD=BD,求折痕BE的长.
如图,在三角形纸片ABC中,∠C=90°,AC=6,折叠该纸片使点C落在AB边上的D点处,折痕BE与AC交于点E.若AD=BD,求折痕BE的长.
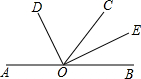 如图,O是直线AB上一点,OC为任一条射线,OD平分∠AOC,OE平分∠BOC.
如图,O是直线AB上一点,OC为任一条射线,OD平分∠AOC,OE平分∠BOC. 如图,在△ABC中有矩形DGFE,点G,F在BC上,点D,E分别在AB,AC上,AH⊥BC交DE于点M.若DG:DE=2:3,BC=15cm,AH=10cm,求矩形DGFE各边的长.
如图,在△ABC中有矩形DGFE,点G,F在BC上,点D,E分别在AB,AC上,AH⊥BC交DE于点M.若DG:DE=2:3,BC=15cm,AH=10cm,求矩形DGFE各边的长.