题目内容
12.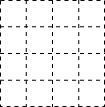 正方形网格中的每个小正方形边长都1,每个小格的顶点叫做格点,以格点为顶点按下列要求画三角形.
正方形网格中的每个小正方形边长都1,每个小格的顶点叫做格点,以格点为顶点按下列要求画三角形.(1)使三角形的三边长分别为3,2$\sqrt{2}$,$\sqrt{5}$;
(2)所画三角形的面积为3(只需写出结果).
分析 (1)利用网格结合勾股定理得出符合题意的答案;
(2)直接利用三角形面积求法得出答案.
解答  解:(1)如图所示:△ABC即为所求;
解:(1)如图所示:△ABC即为所求;
(2)S△ABC=$\frac{1}{2}$×3×2=3.
故答案为:3.
点评 此题主要考查了勾股定理以及三角形面积求法,正确应用勾股定理是解题关键.

练习册系列答案
相关题目
20.长方形相邻两边的长分别是a+3b与2a-b,那么这个长方形的面积是( )
| A. | 2a2-3ab-3b2 | B. | 2a2+5ab+3b2 | C. | 2a2+5ab+3b2 | D. | 2a2+5ab-3b2 |
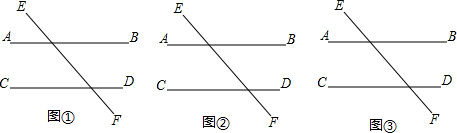
4. 如图,直线a,b被直线c所截,则图中与∠1是同位角的是( )
如图,直线a,b被直线c所截,则图中与∠1是同位角的是( )
 如图,直线a,b被直线c所截,则图中与∠1是同位角的是( )
如图,直线a,b被直线c所截,则图中与∠1是同位角的是( )| A. | ∠2 | B. | ∠3 | C. | ∠4 | D. | ∠5 |
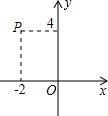 点P在平面直角坐标系的位置如图所示,将点P向下平移a个单位得点P′,若点P′到x轴和y轴的距离均相等,且点P′在第三象限,则a的值是6.
点P在平面直角坐标系的位置如图所示,将点P向下平移a个单位得点P′,若点P′到x轴和y轴的距离均相等,且点P′在第三象限,则a的值是6.