题目内容
14.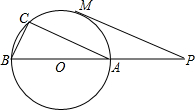 如图,直线PO交⊙O于A,B两点,直径AB=10,弦AC∥PM.点M是$\widehat{AC}$的中点,
如图,直线PO交⊙O于A,B两点,直径AB=10,弦AC∥PM.点M是$\widehat{AC}$的中点,(1)求证:直线PM是⊙O的切线;
(2)若BC=4,求PO的长.
分析 (1)连接OM交AC于N,由垂径定理的推论得出OM⊥AC,AN=CN,再由已知条件得出PM⊥OM,即可得出直线PM是⊙O的切线;
(2)证明ON是△ABC的中位线,由三角形中位线定理得出ON=$\frac{1}{2}$BC=2,证明△OAN∽△OPM,得出对应边成比例$\frac{OA}{PO}=\frac{ON}{OM}$,即可得出PO的长.
解答 (1)证明:连接OM交AC于N,如图所示:
∵点M是$\widehat{AC}$的中点,
∴OM⊥AC,AN=CN,
∵AC∥PM,
∴PM⊥OM,
∴直线PM是⊙O的切线;
(2)解:∵OA=OB,AN=CN,
∴ON是△ABC的中位线,
∴ON=$\frac{1}{2}$BC=2,
∵AB=10,
∴OM=OA=$\frac{1}{2}$AB=5,
∵AC∥PM,
∴△OAN∽△OPM,
∴$\frac{OA}{PO}=\frac{ON}{OM}$,即$\frac{5}{PO}=\frac{2}{5}$,
解得:PO=12.5.
点评 本题考查了切线的判定、垂径定理、三角形中位线定理、相似三角形的判定与性质;熟练掌握切线的判定,证明三角形相似得出比例式是解决问题(2)的关键.

练习册系列答案
相关题目
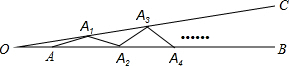 如图,∠BOC=8°,点A在OB上,且OA=1,按下列要求画图:以A为圆心,1为半径向右画弧交OC于点A1,得第1条线段AA1;再以A1为圆心,1为半径向右画弧交OB于点A2,得第2条线段A1A2;再以A2为圆心,1为半径向右画弧交OC于点A3,得第3条线段A2A3;…这样画下去,直到得第n条线段,之后就不能再画出符合要求的线段了,则n的值是( )
如图,∠BOC=8°,点A在OB上,且OA=1,按下列要求画图:以A为圆心,1为半径向右画弧交OC于点A1,得第1条线段AA1;再以A1为圆心,1为半径向右画弧交OB于点A2,得第2条线段A1A2;再以A2为圆心,1为半径向右画弧交OC于点A3,得第3条线段A2A3;…这样画下去,直到得第n条线段,之后就不能再画出符合要求的线段了,则n的值是( )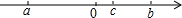 a,b,c在数轴上的位置如图所示,求|c-b|-$\sqrt{(a+b)^{2}}$-$\root{3}{(a+c)^{3}}$的值.
a,b,c在数轴上的位置如图所示,求|c-b|-$\sqrt{(a+b)^{2}}$-$\root{3}{(a+c)^{3}}$的值.