题目内容
如图,∠C=90°,∠CAE=∠ABC,AC=2,BC=3.
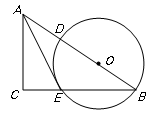
(1)判断AE与⊙O的位置关系,并说明理由;
(2)求OB的长;

(1)判断AE与⊙O的位置关系,并说明理由;
(2)求OB的长;
(1)连接OE,则∠OEB=∠ABC=∠CAE,
∴∠AEC+∠OEB=90°,
∴∠AEO=90°,
∴AE与⊙O相切.
(2)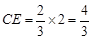 ,
,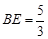 ,
,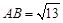 ,
,
∴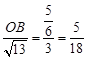 ,
,
∴ 。
。
∴∠AEC+∠OEB=90°,
∴∠AEO=90°,
∴AE与⊙O相切.
(2)
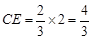 ,
,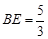 ,
,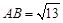 ,
,∴
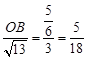 ,
,∴
 。
。(1)连接OE,可证得∠AEO=90°,所以AE与⊙O相切;
(2)作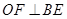 ,则BF=
,则BF=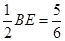 ,易得
,易得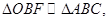 可得
可得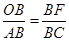 ,即
,即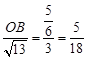 ,所以
,所以 。
。
(2)作
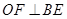 ,则BF=
,则BF=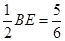 ,易得
,易得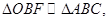 可得
可得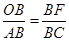 ,即
,即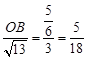 ,所以
,所以 。
。
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
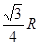

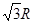
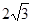 R
R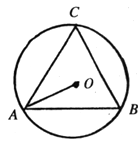
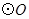 的直径
的直径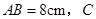 为
为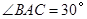 ,则
,则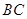 =
=  .
.