题目内容
14.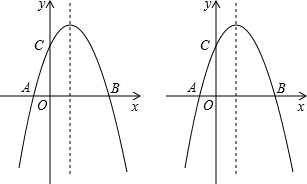 抛物线y=-x2+bx+c经过点A(-1,0)和C(0,3).
抛物线y=-x2+bx+c经过点A(-1,0)和C(0,3).(1)求抛物线的解析式;
(2)点P为抛物线对称轴上一点.
①当PA+PC最小时,求点P的坐标;
②当△PAC是直角三角形时,求点P的坐标.
分析 (1)利用待定系数法即可解决.
(2)求出直线BC与对称轴的交点就是点P.
(3)分三种情形讨论:①当∠ACP1=90°时,求出直线P1C为y=-$\frac{1}{3}$x+3即可.②当∠CAP2=90°,求出直线AP2为y=-$\frac{1}{3}$x-$\frac{1}{3}$即可.③当∠AP3C=90°时,作CE⊥对称轴于E,设P(1,k),由△P3CE∽△AP3F得到$\frac{CE}{{P}_{3}F}$=$\frac{E{P}_{3}}{AF}$,即可解决问题.
解答 解:(1)把点A(-1,0)和C(0,3),代入y=-x2+bx+c得$\left\{\begin{array}{l}{-b+c=0}\\{c=3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{b=2}\\{c=3}\end{array}\right.$.
故抛物线解析式为y=-x2+2x+3.
(2)①设直线BC为y=kx+b,直线BC与对称轴的交点就是点P.
∵抛物线对称轴x=1,点B坐标(3,0),则$\left\{\begin{array}{l}{3k+b=0}\\{b=3}\end{array}\right.$解得$\left\{\begin{array}{l}{k=-1}\\{b=3}\end{array}\right.$,
∴直线BC为y=-x+3,与对称轴的交点为(1,2),
∴点P坐标(1,2).
②当∠ACP1=90°时,
∵直线AC解析式为y=3x+3,
∴直线P1C为y=-$\frac{1}{3}$x+3,
∴点P1(1,$\frac{8}{3}$).
当∠CAP2=90°,直线AP2为y=-$\frac{1}{3}$x-$\frac{1}{3}$,
∴点P2(1,-$\frac{2}{3}$).
当∠AP3C=90°时,作CE⊥对称轴于E,设P(1,k)
由△P3CE∽△AP3F得到$\frac{CE}{{P}_{3}F}$=$\frac{E{P}_{3}}{AF}$,
∴$\frac{1}{k}$=$\frac{3-k}{2}$,
∴k=1或2,
∴点P坐标(1,1)或(1,2).
综上所述点P坐标(1,1)或(1,2)或(1,$\frac{8}{3}$)或(1,-$\frac{2}{3}$).
点评 本题考查二次函数性质、最小值问题、直角三角形,相似三角形的判定和性质等知识,解题的关键是学会待定系数法确定函数解析式,学会分类讨论思想,利用一次函数解决问题,属于中考常考题型.

| A. | $\root{3}{8}$ | B. | 3.14 | C. | $\sqrt{4}$ | D. | -$\sqrt{7}$ |
| A. | $\sqrt{-3}$ | B. | $\sqrt{6}$ | C. | $\root{3}{8}$ | D. | $\sqrt{x}$ |
| A. | a4 | B. | a5 | C. | a6 | D. | a7 |
 如图,已知一张纸片?ABCD,∠B>90°,点E是AB的中点,点G是BC上的一个动点,沿EG将纸片折叠,使点B落在纸片上的点F处,连接AF,则下列各角中与∠BEG不一定相等的是( )
如图,已知一张纸片?ABCD,∠B>90°,点E是AB的中点,点G是BC上的一个动点,沿EG将纸片折叠,使点B落在纸片上的点F处,连接AF,则下列各角中与∠BEG不一定相等的是( )| A. | ∠FEG | B. | ∠EAF | C. | ∠AEF | D. | ∠EFA |
| A. | -9x2y2 | B. | $\frac{9}{16}$x2y2 | C. | $\frac{3}{4}$xy | D. | $\frac{3}{4}$xy3 |
 如图,将线段AB放在边长为1的小正方形网格,点A点B均落在格点上,请只用一把无刻度直尺作图:①线段AB上画出点P,使AP=$\frac{\sqrt{17}}{3}$;②作△ABC,使点C落在格点上,并且使△ABC的面积为6(只作一个);③作线段CD=$\frac{12\sqrt{17}}{17}$.
如图,将线段AB放在边长为1的小正方形网格,点A点B均落在格点上,请只用一把无刻度直尺作图:①线段AB上画出点P,使AP=$\frac{\sqrt{17}}{3}$;②作△ABC,使点C落在格点上,并且使△ABC的面积为6(只作一个);③作线段CD=$\frac{12\sqrt{17}}{17}$.