题目内容
1.天猫网的新时代书店准备购进甲、乙两种图书,已知甲种图书进价比乙种图书贵4元,用3000元购进甲种图书的数量与用2400元购进乙种图书的数量相同.(1)甲、乙两种图书的单价分别为多少元?
(2)若甲种图书每本售价30元,乙种图书每本售价25元,书店欲同时购进两种图书共100本,请写出所获利润y(单位:元)关于甲种图书x(单位:本)的函数解析式;
(3)在(2)的条件下,若书店计划用不超过1800元购进两种图书,且甲种图书至少购进40本,并将所购图书全部销售,共有多少种购进方案?哪一种方案利润最大?
分析 (1)设甲图书的单价为x元/本,则乙图书的单价为(x-4)元/本,根据用3000元购进甲种图书的数量=用2400元购进乙种图书的数量列出方程求解即可;
(2)由于购买甲种图书x本,则购买乙种图书(100-x)本,根据:总利润=甲种图书的总利润+乙种图书的总利润可列函数关系式;
(3)根据用不超过1800元购进两种图书,且甲种图书至少购进40本列出不等式组,解不等式组求出解集,从而确定方案,进而求出利润最大的方案.
解答 解:(1)设甲图书的单价为x元/本,则乙图书的单价为(x-4)元/本,根据题意,
得:$\frac{3000}{x}$=$\frac{2400}{x-4}$,
解得:x=20,
经检验x=20是原方程的根,
则x-4=16,
答:甲图书的单价为20元/本,乙图书的单价为16元/本;
(2)根据题意,有:
y=(30-20)x+(25-16)(100-x)=x+900;
(3)根据题意,得:$\left\{\begin{array}{l}{20x+16(100-x)≤1800}\\{x≥40}\end{array}\right.$,
解得:40≤x≤50,
∵x需取整数,
∴x的值可以是:40,41,42,43,44,45,46,47,48,49,50,
故购买方案有11种.
∵y=x+900,k=1>0,
∴y随x的增大而增大,
∴x取最大值50时,y有最大值,
故购买方案有11种.利润最大的方案是:购买甲种图书50本,购买乙种图书50本.
点评 本题考查了一次函数的应用,分式方程的应用,一元一次不等式组的应用,理解题意找到题目蕴含的相等关系或不等关系是解应用题的关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
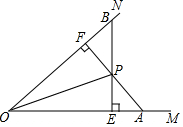 如图,已知点P是∠MON平分线上的一点,PE⊥OM,垂足为E,PF⊥ON,垂足为F,延长FP,交OM于点A,延长EP,交ON于点B,求证:PA=PB.
如图,已知点P是∠MON平分线上的一点,PE⊥OM,垂足为E,PF⊥ON,垂足为F,延长FP,交OM于点A,延长EP,交ON于点B,求证:PA=PB. 如图,∠AOB的平分线上有一点C,CD⊥OA于点D,若CD=3,则点C到OB的距离为3.
如图,∠AOB的平分线上有一点C,CD⊥OA于点D,若CD=3,则点C到OB的距离为3.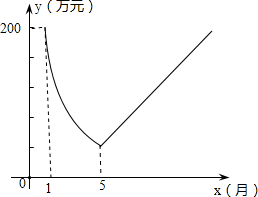 我省某化工厂2013年1月的利润为200万元,若设2013年1月为第一个月,第x个月的利润为y万元;由于污染问题,该厂决定从2013年1月底适当限产,并投入资金进行新技术改造,导致月利润明显下降.从1月底到5月,y与x成反比例关系.到5月底,新技术改造任务顺利完成,从这时起,该厂每月利润比前月增加20万元(如图).
我省某化工厂2013年1月的利润为200万元,若设2013年1月为第一个月,第x个月的利润为y万元;由于污染问题,该厂决定从2013年1月底适当限产,并投入资金进行新技术改造,导致月利润明显下降.从1月底到5月,y与x成反比例关系.到5月底,新技术改造任务顺利完成,从这时起,该厂每月利润比前月增加20万元(如图). 如图,?ABCD中,点E、F在直线BD上,连接AF、CE,不添加任何辅助线,请添加一个条件DF=BE,使AF=CE(填一个即可)
如图,?ABCD中,点E、F在直线BD上,连接AF、CE,不添加任何辅助线,请添加一个条件DF=BE,使AF=CE(填一个即可)