题目内容
8. 已知,如图,AB=AC,AD=AE,AB,DC相交于点M,AC,BE相交于点N,∠DAB=∠EAC,求证:AM=AN.
已知,如图,AB=AC,AD=AE,AB,DC相交于点M,AC,BE相交于点N,∠DAB=∠EAC,求证:AM=AN.
分析 可先证明△ACD与△ABE全等,得出∠D=∠E,进而证得△ADM≌△AEN,结论可得.
解答 证明:∵∠DAB=∠EAC,
∴∠DAB+∠BAC=∠EAC+∠BAC,
即∠DAC=∠AEB,
在△ACD与△ABE中,$\left\{\begin{array}{l}{AD=AE}\\{∠DAC=∠EAB}\\{AC=AB}\end{array}\right.$,
∴△ACD≌△ABE,
∴∠D=∠E,
在△ADM与△AEN中,$\left\{\begin{array}{l}{∠D=∠E}\\{AD=AE}\\{∠DAB=∠EAC}\end{array}\right.$,
∴△ADM≌△AEN,
∴AM=AN.
点评 本题考查了全等三角形的判定和性质,熟练掌握全等三角形的判定和性质是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.下列图形中,不属于中心对称图形的是( )
| A. | 圆 | B. | 等边三角形 | C. | 平行四边形 | D. | 线段 |
13.二元一次方程3x-2y=1的不超过10的正整数解共有( )组.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
20.任意大于1的正整数m的三次幂均可“分裂”成m个连续奇数的和,如:23=3+5,33=7+9+11,43=13+15+17+19,…按此规律,若m3分裂后其中有一个奇数是2015,则m的值是( )
| A. | 46 | B. | 45 | C. | 44 | D. | 43 |
17. 如图,已知AB∥CD,若∠A=25°,∠E=40°,则∠C等于( )
如图,已知AB∥CD,若∠A=25°,∠E=40°,则∠C等于( )
 如图,已知AB∥CD,若∠A=25°,∠E=40°,则∠C等于( )
如图,已知AB∥CD,若∠A=25°,∠E=40°,则∠C等于( )| A. | 40° | B. | 65° | C. | 115° | D. | 25° |
 如图,∠1=∠2,∠C=∠D
如图,∠1=∠2,∠C=∠D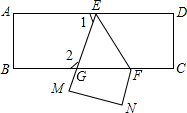 把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G,D、C分别在M、N的位置上,若∠EFG=55°,求:
把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G,D、C分别在M、N的位置上,若∠EFG=55°,求: