题目内容
2. 如图,在正方形ABCD中,F是DC的中点,E是BC上的一点,且EC=$\frac{1}{4}$BC=1,试判断AF与EF是否垂直,并说明理由.
如图,在正方形ABCD中,F是DC的中点,E是BC上的一点,且EC=$\frac{1}{4}$BC=1,试判断AF与EF是否垂直,并说明理由.
分析 分别计算AF,EF,AE的值,根据三角形三边长和勾股定理的逆定理可以判定△AEF为直角三角形,即可证明AF⊥EF.
解答  解:连接AE,AF与EF垂直,
解:连接AE,AF与EF垂直,
∵ABCD是正方形,EC=$\frac{1}{4}$BC=1,
∴AD=CD=BC=4,∠D=∠C=∠B=90°.
∵F为DC中点,
∴DF=FC=2,BE=3,
由勾股定理可得:AF2=42+22=20,EF2=12+22=5,AE2=32+42=25,
AE2=AF2+EF2,
∴AF⊥EF.
点评 本题考查了勾股定理在直角三角形中的运用,考查了正方形各边长相等、各内角为直角的性质,考查了勾股定理的逆定理判定直角三角形的方法,本题中判定△AEF为直角三角形是解题的关键.

练习册系列答案
相关题目
13.某商品的进价是80元,打8折售出后,仍可获利10%,你认为标在标签上的价格为( )
| A. | 110元 | B. | 120元 | C. | 150元 | D. | 160元 |
 如图,边长为a的正六边形螺帽在桌面上滚动(没有滑动)一周,则它的中心O点所经过的路径长为2πa.
如图,边长为a的正六边形螺帽在桌面上滚动(没有滑动)一周,则它的中心O点所经过的路径长为2πa.

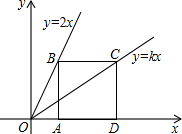 如图,已知四边形ABCD是正方形,点B,C分别在两条直线y=2x和y=kx上,点A,D是x轴上两点.
如图,已知四边形ABCD是正方形,点B,C分别在两条直线y=2x和y=kx上,点A,D是x轴上两点.