Question

5．如图，在矩形ABCD中，AD=25，AB=12，点E、F分别是AD、BC上的点，且DE=CF=9，连接EF、DF、AF．取AF的中点为G，连接BG，将△BFG沿BC方向平移，当点F到达点C时停止平移，然后将△GFB绕C点顺时针旋转α（0°＜α＜90°），得到△B₁CG₁（点G的对应点为G₁，点B的对应点为B₁），在旋转过程中，直线B₁G₁与直线EF、FD分别相交M、N，当△FMN是等腰三角形，且FM=FN时，线段DN的长为$\frac{60-16\sqrt{10}}{5}$．

Answer 1

分析 如图，作FL⊥BG于L，FH⊥MN于H，CK⊥MN于K，CR⊥FH于R．FH交ED于T，作TQ⊥DF于Q，先求出FL、CK，设TE=TQ=x，在RT△TQD中，由TQ²+QD²=TD²，求出x，
由△FET∽△CFR，得$\frac{ET}{FR}$=$\frac{FT}{CF}$，求出RF，再由cos∠HFN=$\frac{FH}{FN}$=$\frac{EF}{TF}$，求出FN即可解决问题．

解答 解：如图，作FL⊥BG于L，FH⊥MN于H，CK⊥MN于K，CR⊥FH于R．FH交ED于T，作TQ⊥DF于Q．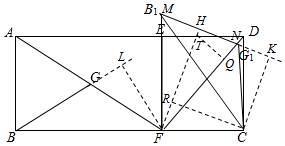

∵四边形ABCD是矩形，
∴∠ABC=∠ADC=∠BCD=90°，AB=CD=12，AD=CF=25，
∵DE=CF=9，又∵DE∥CF，
∴四边形DEFC是平行四边形，
∵∠EDC=90°，
∴四边形DEFC是矩形，同理四边形AEFB是矩形，
∴DF=$\sqrt{C{F}^{2}+C{D}^{2}}$=$\sqrt{{9}^{2}+1{2}^{2}}$=15，AF=$\sqrt{A{B}^{2}+B{F}^{2}}$=$\sqrt{1{2}^{2}+1{6}^{2}}$=20，
∵G为AF的中点，
∴BG=$\frac{1}{2}$AF=10，
∵AG=GF，
∴S_△BGF=$\frac{1}{2}$S_△ABF=48=$\frac{1}{2}$•BG•LF，
∴FL=$\frac{48}{5}$，
∵CK=FL，
∴CK=$\frac{48}{5}$，
∵FM=FN，FH⊥MN，CK⊥MN，CR⊥FH，
∴∠RHK=∠HKC=∠KCR=90°，
∴四边形RHKC是矩形，
∴RH=CK=$\frac{48}{5}$，
∴∠MFH=∠NFH，
∴TE=TQ，设TE=TQ=x，
在RT△TQD中，∵TQ²+QD²=TD²，
∴x²+3²=（9-x）²，
∴x=4，
∴FT=$\sqrt{E{F}^{2}+E{T}^{2}}$=4$\sqrt{10}$，
∵∠EFT+∠CFR=90°，∠CFR+∠FCR=90°，
∴∠EFT=∠FCR，∵∠FET=∠CFR=90°，
∴△FET∽△CFR，
∴$\frac{ET}{FR}$=$\frac{FT}{CF}$，
∴$\frac{4}{RF}$=$\frac{4\sqrt{10}}{9}$，
∴RF=$\frac{9\sqrt{10}}{10}$，
∴FH=FR+RH=$\frac{96+9\sqrt{10}}{10}$，
∵∠HFN=∠HFM，
∴cos∠HFN=$\frac{FH}{FN}$=$\frac{EF}{TF}$，
∴$\frac{\frac{96+6\sqrt{5}}{5}}{FN}$=$\frac{12}{6\sqrt{5}}$，
∴FN=$\frac{16\sqrt{10}+15}{5}$，
∴DN=DF-FN=$\frac{60-16\sqrt{10}}{5}$．
故答案为：$\frac{60-16\sqrt{10}}{5}$．

点评 本题考查几何变换综合题、矩形的性质、勾股定理、相似三角形的判定和性质等知识，解题的关键是学会正确画出图形，学会添加常用辅助线，构造相似三角形解决问题，属于中考填空题中的压轴题．