题目内容
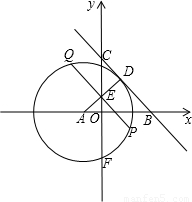
如图,过y轴上任意一点P,作x轴的平行线,分别与反比例函数 的图象交于A点和B点,若C为x轴上任意一点,连接AC,BC,则△ABC的面积为( )
的图象交于A点和B点,若C为x轴上任意一点,连接AC,BC,则△ABC的面积为( )
A.3
B.4
C.5
D.6
【答案】分析:先设P(0,b),由直线AB∥x轴,则A,B两点的纵坐标都为b,而A,B分别在反比例函数 的图象上,可得到A点坐标为(-
的图象上,可得到A点坐标为(- ,b),B点坐标为(
,b),B点坐标为( ,b),从而求出AB的长,然后根据三角形的面积公式计算即可.
,b),从而求出AB的长,然后根据三角形的面积公式计算即可.
解答:解:设P(0,b),
∵直线AB∥x轴,
∴A,B两点的纵坐标都为b,
而点A在反比例函数y=- 的图象上,
的图象上,
∴当y=b,x=- ,即A点坐标为(-
,即A点坐标为(- ,b),
,b),
又∵点B在反比例函数y= 的图象上,
的图象上,
∴当y=b,x= ,即B点坐标为(
,即B点坐标为( ,b),
,b),
∴AB= -(-
-(- )=
)= ,
,
∴S△ABC= •AB•OP=
•AB•OP=
 •b=3.
•b=3.
故选A.
点评:本题考查了点在函数图象上,点的横纵坐标满足函数图象的解析式.也考查了与坐标轴平行的直线上的点的坐标特点以及三角形的面积公式.
 的图象上,可得到A点坐标为(-
的图象上,可得到A点坐标为(- ,b),B点坐标为(
,b),B点坐标为( ,b),从而求出AB的长,然后根据三角形的面积公式计算即可.
,b),从而求出AB的长,然后根据三角形的面积公式计算即可.解答:解:设P(0,b),
∵直线AB∥x轴,
∴A,B两点的纵坐标都为b,
而点A在反比例函数y=-
 的图象上,
的图象上,∴当y=b,x=-
 ,即A点坐标为(-
,即A点坐标为(- ,b),
,b),又∵点B在反比例函数y=
 的图象上,
的图象上,∴当y=b,x=
 ,即B点坐标为(
,即B点坐标为( ,b),
,b),∴AB=
 -(-
-(- )=
)= ,
,∴S△ABC=
 •AB•OP=
•AB•OP=
 •b=3.
•b=3.故选A.
点评:本题考查了点在函数图象上,点的横纵坐标满足函数图象的解析式.也考查了与坐标轴平行的直线上的点的坐标特点以及三角形的面积公式.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
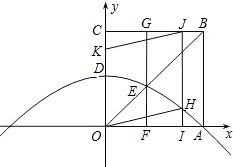 如图,在平面直角坐标系中,正方形OABC的边长是2.O为坐标原点,点A在x的正半轴上,点C在y的正半轴上.一条抛物线经过A点,顶点D是OC的中点.
如图,在平面直角坐标系中,正方形OABC的边长是2.O为坐标原点,点A在x的正半轴上,点C在y的正半轴上.一条抛物线经过A点,顶点D是OC的中点. 如图,在直角坐标系中,点A,B,C的坐标分别为(-1,0),(3,0),(0,3),D(1,a)在直线BC上,⊙A是以A为圆心,AD为半径的圆.
如图,在直角坐标系中,点A,B,C的坐标分别为(-1,0),(3,0),(0,3),D(1,a)在直线BC上,⊙A是以A为圆心,AD为半径的圆. (2013•启东市一模)如图所示,过y轴正半轴上的任意一点P,作x轴的平行线,分别与反比例函数
(2013•启东市一模)如图所示,过y轴正半轴上的任意一点P,作x轴的平行线,分别与反比例函数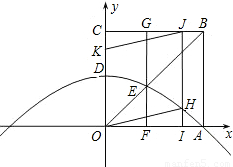 如图,在平面直角坐标系中,正方形OABC的边长是2.O为坐标原点,点A在x的正半轴上,点C在y的正半轴上.一条抛物线经过A点,顶点D是OC的中点.
如图,在平面直角坐标系中,正方形OABC的边长是2.O为坐标原点,点A在x的正半轴上,点C在y的正半轴上.一条抛物线经过A点,顶点D是OC的中点.