题目内容
16.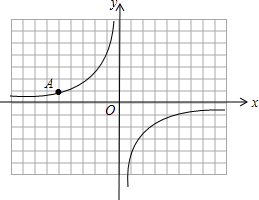 如图,在每格为1个单位的正方形网格中建立直角坐标系,反比例函数y=$\frac{k}{x}$的图象经过格点A.
如图,在每格为1个单位的正方形网格中建立直角坐标系,反比例函数y=$\frac{k}{x}$的图象经过格点A.(1)请写出点A的坐标、反比例函数y=$\frac{k}{x}$的解析式;
(2)若点B(m,y1)、C(n,y2)(2<m<n)都在函数y=$\frac{k}{x}$的图象上,试比较y1与y2的大小.
分析 (1)由图可得点A的坐标为:(-5,1),又由反比例函数y=$\frac{k}{x}$经过A点,利用待定系数法即可求得反比例函数解析式;
(2)由反比例函数的性质:k<0时,在每个象限内,y随x的增大而增大,因为2<m<n,所以B,C都在第四象限,所以y1<y2.
解答 解:(1)由表得知A(-5,1),
∵反比例函数y=$\frac{k}{x}$的图象经过格点A.
∴k=-5,
∴反比例函数y=$\frac{k}{x}$的解析式为:y=-$\frac{5}{x}$;
(2)∵k=-5<0,
∴在每个象限内,y随x的增大而增大,
∵2<m<n,
∴y1<y2.
点评 此题属于反比例函数综合题,考查了待定系数求函数解析式、反比例函数的性质,掌握反比例函数的性质是解题的关键.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
6.在一次献爱心的捐赠活动中,某班45名同学捐款金额统计如下:
在这次活动中,该班同学捐款金额的众数和中位数分别是50,50.
| 金额(元) | 20 | 30 | 35 | 50 | 100 |
| 学生数(人) | 5 | 10 | 5 | 15 | 10 |
11.下列四个图形中,既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
1.下列从左边到右边的变形,是因式分解的是( )
| A. | (a-1)(a-2)=a2-3a+2 | B. | a2-3a+2=(a-1)(a-2) | ||
| C. | (a-1)2+(a-1)=a2-a | D. | a2-3a+2=(a-1)2-(a-1) |
6.地球绕太阳每小时转动经过的路程约为110000米,将110000用科学记数法表示为( )
| A. | 11×104 | B. | 0.11×107 | C. | 1.1×106 | D. | 1.1×105 |
 三角形中有3个角、3条边共6个元素,由其中的已知元素,求出所有未知元素的过程,叫做解三角形.
三角形中有3个角、3条边共6个元素,由其中的已知元素,求出所有未知元素的过程,叫做解三角形.