题目内容
8. 三角形中有3个角、3条边共6个元素,由其中的已知元素,求出所有未知元素的过程,叫做解三角形.
三角形中有3个角、3条边共6个元素,由其中的已知元素,求出所有未知元素的过程,叫做解三角形.已知△ABC中,AB=$\sqrt{2}$,∠B=45°,BC=1+$\sqrt{3}$,解△ABC.
分析 过点A作AD⊥BC,垂足为D,解直角三角形求出BD、AD,求出CD,解直角三角形求出∠C,AC,即可求出答案.
解答 解:过点A作AD⊥BC,垂足为D,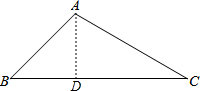
在Rt△ADB中,∠ADB=90°,∠B=45°,AB=$\sqrt{2}$,
则cos∠B=$\frac{BD}{AB}$.
∴AD=BD=AB×cos 45°=$\sqrt{2}$×cos 45°=1,
在Rt△ADC中,∠ADC=90°,CD=BC-BD=1+$\sqrt{3}$-1=$\sqrt{3}$,
则tan∠C=$\frac{AD}{CD}$=$\frac{1}{\sqrt{3}}$=$\frac{\sqrt{3}}{3}$,
∴∠C=30°,
∴AC=$\sqrt{{1}^{2}+(\sqrt{3})^{2}}$=2,∠BAC=180°-45°-30°=105°.
点评 本题考查了解直角三角形,勾股定理,特殊角的三角函数值的应用,能求出各个角的度数和求出各个边的长是解此题的关键,难度适中.

练习册系列答案
相关题目
18.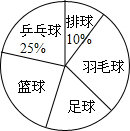 某中学为合理安排体育活动,在全校喜欢乒乓球、排球、羽毛球、足球、篮球五种球类运动的1000名学生中,随机抽取了若干名学生进行调查,了解学生最喜爱的球类运动,每人只能在这五种球类运动中选择一种,调查结果统计如表、如图所示:
某中学为合理安排体育活动,在全校喜欢乒乓球、排球、羽毛球、足球、篮球五种球类运动的1000名学生中,随机抽取了若干名学生进行调查,了解学生最喜爱的球类运动,每人只能在这五种球类运动中选择一种,调查结果统计如表、如图所示:
解答下列问题:
(1)求a和b的值;
(2)试估计上述1000名学生中最喜欢羽毛球运动的人数.
 某中学为合理安排体育活动,在全校喜欢乒乓球、排球、羽毛球、足球、篮球五种球类运动的1000名学生中,随机抽取了若干名学生进行调查,了解学生最喜爱的球类运动,每人只能在这五种球类运动中选择一种,调查结果统计如表、如图所示:
某中学为合理安排体育活动,在全校喜欢乒乓球、排球、羽毛球、足球、篮球五种球类运动的1000名学生中,随机抽取了若干名学生进行调查,了解学生最喜爱的球类运动,每人只能在这五种球类运动中选择一种,调查结果统计如表、如图所示:| 球类名称 | 人数 |
| 乒乓球 | a |
| 排球 | 12 |
| 羽毛球 | 36 |
| 足球 | 18 |
| 篮球 | b |
(1)求a和b的值;
(2)试估计上述1000名学生中最喜欢羽毛球运动的人数.
19.计算8+6÷(-2)的结果是( )
| A. | -7 | B. | -5 | C. | 5 | D. | 7 |
20.已知一组数据:-3,6,2,-1,0,4,则这组数据的中位数是( )
| A. | 1 | B. | $\frac{4}{3}$ | C. | 0 | D. | 2 |
17.小明在”百度”搜索引擎中输入”钓鱼岛最新消息”,能搜索到与之相关的结果个数约为564000,这个数用科学记数法表示为( )
| A. | 5.64×104 | B. | 56.4×104 | C. | 5.64×105 | D. | 0.564×106 |
18.点P(4,3)所在的象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
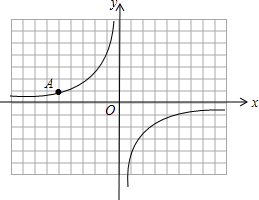 如图,在每格为1个单位的正方形网格中建立直角坐标系,反比例函数y=$\frac{k}{x}$的图象经过格点A.
如图,在每格为1个单位的正方形网格中建立直角坐标系,反比例函数y=$\frac{k}{x}$的图象经过格点A.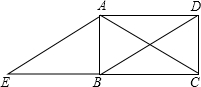 如图,在平行四边形ABCD中,过点A作AE∥BD交CB的延长线于点E,且AE=AC,判断四边形ABCD的形状,并说明理由.
如图,在平行四边形ABCD中,过点A作AE∥BD交CB的延长线于点E,且AE=AC,判断四边形ABCD的形状,并说明理由.