题目内容
5. 如图,四边形ABCD是长方形,尺寸如图所示:
如图,四边形ABCD是长方形,尺寸如图所示:(1)求阴影部分的面积;
(2)若a=30,b=10,c=22,d=9,求阴影部分的面积;
(3)若∠1=∠2,那么∠3与∠4有怎样的关系,并说明理由.
分析 (1)阴影部分面积等于矩形面积减去两个直角三角形面积,求出即可;
(2)把a,b,c,d的值代入计算即可求出值;
(3)互余,利用同角的余角相等验证即可.
解答 解:(1)根据题意得:S=ac-$\frac{1}{2}$(c-d)(a-b)-$\frac{1}{2}$bc=ac-$\frac{1}{2}$(ac-bc-ad+bd)=$\frac{1}{2}$ac+$\frac{1}{2}$bc+$\frac{1}{2}$ad-$\frac{1}{2}$bd;
(2)当a=30,b=10,c=22,d=9时,S=330+110+135-45=530;
(3)∠3+∠4=90°,理由为:
∵∠1+∠3=90°,∠1=∠2,
∴∠3+∠2=90°,
∵∠2=∠4,
∴∠3+∠4=90°.
点评 此题考查了整式的混合运算,以及平行线的性质,熟练掌握运算法则是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.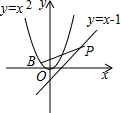 如图,点P在直线y=x-1上,若存在过点P的直线交抛物线y=x2于A、B两点,且PA=AB,则称点P为“优点”,下列结论中正确的是( )
如图,点P在直线y=x-1上,若存在过点P的直线交抛物线y=x2于A、B两点,且PA=AB,则称点P为“优点”,下列结论中正确的是( )
 如图,点P在直线y=x-1上,若存在过点P的直线交抛物线y=x2于A、B两点,且PA=AB,则称点P为“优点”,下列结论中正确的是( )
如图,点P在直线y=x-1上,若存在过点P的直线交抛物线y=x2于A、B两点,且PA=AB,则称点P为“优点”,下列结论中正确的是( )| A. | 直线y=x-1上的所有点都是“优点” | |
| B. | 直线y=x-1上仅有有限个点是“优点” | |
| C. | 直线y=x-1上的所有点都不是“优点” | |
| D. | 直线y=x-1上有无穷多个点(不是所有的点)是“优点” |
 我市某中学开设“生物第二课堂”,在校园内开辟出一块L型的空闲土地,准备进行植物种植研究,按如图所示的虚线分成了面积相等的两个梯形,这两个梯形的上底都是am,下底都是bm,高都是(b-a)m,请你算一算这块土地的面积是多少?并求出当a=20m,b=30m时这块土地的面积.
我市某中学开设“生物第二课堂”,在校园内开辟出一块L型的空闲土地,准备进行植物种植研究,按如图所示的虚线分成了面积相等的两个梯形,这两个梯形的上底都是am,下底都是bm,高都是(b-a)m,请你算一算这块土地的面积是多少?并求出当a=20m,b=30m时这块土地的面积. 一副直角三角板如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,∠E=45°,∠A=60°,BC=10$\sqrt{3}$,试求CD的长.
一副直角三角板如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,∠E=45°,∠A=60°,BC=10$\sqrt{3}$,试求CD的长.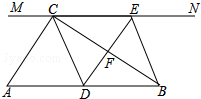 如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE.
如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE. 如图,修公路遇到一座山,于是要修一条隧道.为了加快施工进度,想在小山的另一侧同时施工.为了使山的另一侧的开挖点C在AB的延长线上,设想过C点作直线AB的垂线L,过点B作一直线(在山的旁边经过),与L相交于D点,经测量∠ABD=135°,BD=800米,求直线L上距离D点多远的C处开挖?(结果保留根号)
如图,修公路遇到一座山,于是要修一条隧道.为了加快施工进度,想在小山的另一侧同时施工.为了使山的另一侧的开挖点C在AB的延长线上,设想过C点作直线AB的垂线L,过点B作一直线(在山的旁边经过),与L相交于D点,经测量∠ABD=135°,BD=800米,求直线L上距离D点多远的C处开挖?(结果保留根号) 如图,等边三角形ABC内接于半径为1的⊙O,以BC为一边作⊙O的内接矩形BCDE,则矩形BCDE的面积为$\sqrt{3}$.
如图,等边三角形ABC内接于半径为1的⊙O,以BC为一边作⊙O的内接矩形BCDE,则矩形BCDE的面积为$\sqrt{3}$.