题目内容
19.(1)阅读理解:如图1,等边△ABC内有一点P若点P到顶点A,B,C的距离分别为3,4,5,求∠APB的大小.
思路点拨:考虑到PA,PB,PC不在一个三角形中,采用转化与化归的数学思想,可以将△ABP绕顶点A逆时针旋转60°到△ACP′处,此时△ACP′≌△ABP,这样,就可以利用全等三角形知识,结合已知条件,将三条线段的长度转化到一个三角形中,从而求出∠APB的度数.请你写出完整的解题过程.
(2)变式拓展:请你利用第(1)题的解答思想方法,解答下面问题:
已知如图2,△ABC中,∠CAB=90°,AB=AC,E、F为BC上的点且∠EAF=45°,BE=5,CF=4,求EF的大小.
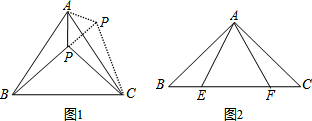
分析 (1)根据等边三角形的性质得出AB=AC,∠BAC=60°,根据旋转得出△ACP′≌△ABP,求出PA=P′A=3,PB=P′C=4,∠BAP=∠CAP′,求出∠P′AP=∠BAC=60°,推出△PAP′是等边三角形,求出PP′=P′A=3,根据勾股定理的逆定理求出∠PP′C=90°,即可得出答案;
(2)根据旋转得出△ACE′≌△ABE,根据全等得出AE=AE′,BE=CE′,∠E′AC=′BAE,求出∠FAE′=∠EAF,根据全等三角形的判定推出△AEF≌△AE′F,推出FE=FE′,根据勾股定理求出E′F即可.
解答 
解:(1)∵三角形ABC是等边三角形,
∴AB=AC,∠BAC=60°,
如图1,将△ABP绕顶点A逆时针旋转60°到△ACP′处,
则△ACP′≌△ABP,
∴PA=P′A=3,PB=P′C=4,∠BAP=∠CAP′,
∴∠P′AP=∠PAC+∠CAP′=∠PAC+∠BAP=∠BAC=60°,
∴△PAP′是等边三角形,
∴PP′=P′A=3,
在△PP′C中,PP'2+P′C2=9+15=25=PC2,
∴△PP′C是直角三角形,
∴∠PP′C=90°,
∴∠APB=∠AP′C=60°+90°=150°;
(2)将△ABE绕顶点A逆时针旋转90°到△ACE′处,
则△ACE′≌△ABE,
∴AE=AE′,BE=CE′,∠E′AC=′BAE,
∵∠BAC=90°,∠EAF=45°,
∴∠BAE+∠CAF=45°,
∠FAE′=∠E′AC+∠FAC=∠BAE+∠FAC=45°=∠EAF,
在△AEF和△AE′F中,
$\left\{\begin{array}{l}{AE=AE′}\\{∠EAF=∠E′AF}\\{AF=AF}\end{array}\right.$,
∴△AEF≌△AE′F,
∴FE=FE′,
∵∠BAC=90°,AB=AC,
∴∠B=∠ACB=45°,
∴∠E′CA=∠B=45°,
∴∠E′CF=45°+45°=90°,
在Rt△E′FC中,E′C2+FC2=E′F2,
∴EF2=BE2+CF2=52+42=41,
∴EF=$\sqrt{41}$.
点评 本题考查了旋转的性质,全等三角形的性质和判定,勾股定理和勾股定理的逆定理的应用,能综合运用性质进行推理是解此题的关键,证明过程类似.

 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案| A. | x≥1 | B. | x<-2 | C. | 1≤x<-2 | D. | x≥1或x<-2 |
| A. |  | B. |  | C. |  | D. |  |
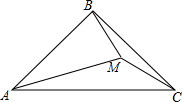 如图,等腰△ABC中,AB=CB,M为ABC内一点,∠MAC+∠MCB=∠MCA=30°
如图,等腰△ABC中,AB=CB,M为ABC内一点,∠MAC+∠MCB=∠MCA=30° 如图,线段AB的长为1,C在AB上,D在AC上,且AC2=BC•AB,AD2=CD•AC,AE2=DE•AD,则AE的长为$\sqrt{5}$-2.
如图,线段AB的长为1,C在AB上,D在AC上,且AC2=BC•AB,AD2=CD•AC,AE2=DE•AD,则AE的长为$\sqrt{5}$-2.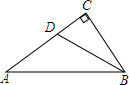 如图,△ABC,∠C=90°,∠ABC=60°,BD平分∠ABC,若AD=8,求CD的长.
如图,△ABC,∠C=90°,∠ABC=60°,BD平分∠ABC,若AD=8,求CD的长.