题目内容
5.在某一时刻,测得身高为1.5m的小明的影长为3m,同时测得一幢高楼的影长为90m,则这幢高楼的高度为45m.分析 由于光线是平行的,影长都在地面上,那么可得高楼与影长构成的三角形和身高和影长构成的三角形相似,利用对应边成比例可得楼高.
解答 解:∵光线是平行的,影长都在地面上,
∴光线和影长组成的角相等;楼高和身高与影长构成的角均为直角,
∴高楼与影长构成的三角形和身高和影长构成的三角形相似,
设楼的高度为x米,$\frac{x}{90}$=$\frac{1.5}{3}$,
解得x=45.
故答案为:45.
点评 此题主要考查相似三角形的应用,关键是掌握两角对应相等的两三角形相似;相似三角形的对应边成比例.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13.设$\sqrt{2}=a,\sqrt{3}=b$,用含a、b的式子表示$\sqrt{0.54}$,下列表示正确的是( )
| A. | $\frac{3ab}{10}$ | B. | 3ab | C. | $\frac{{{a^2}{b^2}}}{10}$ | D. | $\frac{{{a^3}b}}{10}$ |
10.已知等腰三角形的两边分别为3和7,则此三角形的第三边可能是( )
| A. | 3 | B. | 4 | C. | 6 | D. | 7 |
15.计算(-a3)2的结果是( )
| A. | a6 | B. | -a6 | C. | a5 | D. | -a5 |
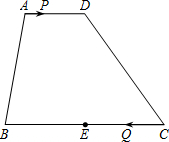 如图,在梯形ABCD中,AD∥BC,AD=6,BC=16,E是BC的中点.点P以每秒1个单位长度的速度从点A出发,沿AD向点D运动;点Q同时以每秒8个单位长度的速度从点C出发,沿CB向点B运动.点P停止运动时,点Q也随之停止运动.当运动时间t=$\frac{2}{7}$或$\frac{14}{9}$秒时,以点P、Q、E、D为顶点的四边形是平行四边形.
如图,在梯形ABCD中,AD∥BC,AD=6,BC=16,E是BC的中点.点P以每秒1个单位长度的速度从点A出发,沿AD向点D运动;点Q同时以每秒8个单位长度的速度从点C出发,沿CB向点B运动.点P停止运动时,点Q也随之停止运动.当运动时间t=$\frac{2}{7}$或$\frac{14}{9}$秒时,以点P、Q、E、D为顶点的四边形是平行四边形.