题目内容
4.△ABC中,∠A,∠B,∠C所对的边分别是a,b,c,满足下列条件的△ABC,不是直角三角形的是( )| A. | a:b:c=1:$\sqrt{2}$:1 | B. | ∠A:∠B:∠C=3:4:5 | C. | (a+b)(a-b)=c2 | D. | ∠A:∠B:∠C=1:2:3 |
分析 运用直角三角形的判定方法,当一个角是直角时,或两边的平方和等于第三条边的平方,也可得出它是直角三角形.分别判定即可.
解答 解:A、∵12+12=($\sqrt{2}$)2,∴是直角三角形,不符合题意;
B、设三角形的三角分别为3x°,4x°,5x°,3x+4x+5x=180,解得x=15,15°×3=45°,15°×4=60°,15°×5=75°,所以不是直角三角形,符合题意;
C、∵(a+b)(a-b)=c2,a2=b2+c2,∴∠A=90°,∴是直角三角形,不符合题意;
D、设三角形的三角分别为x°,2x°,3x°,x+2x+3x=180,解得x=30,30°×1=30°,30°×2=60°,30°×3=90°,所以是直角三角形,不符合题意.
故选:B.
点评 此题主要考查了勾股定理逆定理以及三角形的内角和定理,灵活的应用直角三角形的判定方法是解决问题的关键.

练习册系列答案
相关题目
15.下列调查中,最适合采用抽样调查方式的是( )
| A. | 值日老师调查各班学生的出勤情况 | |
| B. | 调查凉山州中学生参加体育锻炼的时间 | |
| C. | 了解某班女学生的身高情况 | |
| D. | 了解全班同学的课外读书时间 |
9.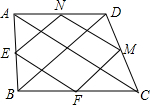 在四边形ABCD中,连接对角线AC,BD,E、F、M、N分别是AB、BC、CD、AD的中点,连接EF、FM、MN、EN,下列条件中,能使四边形EFMN是菱形的是( )
在四边形ABCD中,连接对角线AC,BD,E、F、M、N分别是AB、BC、CD、AD的中点,连接EF、FM、MN、EN,下列条件中,能使四边形EFMN是菱形的是( )
 在四边形ABCD中,连接对角线AC,BD,E、F、M、N分别是AB、BC、CD、AD的中点,连接EF、FM、MN、EN,下列条件中,能使四边形EFMN是菱形的是( )
在四边形ABCD中,连接对角线AC,BD,E、F、M、N分别是AB、BC、CD、AD的中点,连接EF、FM、MN、EN,下列条件中,能使四边形EFMN是菱形的是( )| A. | AB=BC | B. | AB⊥BC | C. | AC⊥BD | D. | AC=BD |
14.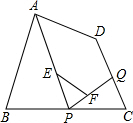 如图,在四边形ABCD中,Q是CD上的一定点,P是BC上的一动点,点E、F分别是PA、PQ的中点,当点P在BC上移动时,线段EF的长度( )
如图,在四边形ABCD中,Q是CD上的一定点,P是BC上的一动点,点E、F分别是PA、PQ的中点,当点P在BC上移动时,线段EF的长度( )
 如图,在四边形ABCD中,Q是CD上的一定点,P是BC上的一动点,点E、F分别是PA、PQ的中点,当点P在BC上移动时,线段EF的长度( )
如图,在四边形ABCD中,Q是CD上的一定点,P是BC上的一动点,点E、F分别是PA、PQ的中点,当点P在BC上移动时,线段EF的长度( )| A. | 先变大,后变小 | B. | 保持不变 | C. | 先变小,后变大 | D. | 无法确定 |
 如图,在⊙O中,$\widehat{AB}$=$\widehat{CD}$,∠DCB=28°,则∠ABC=28度.
如图,在⊙O中,$\widehat{AB}$=$\widehat{CD}$,∠DCB=28°,则∠ABC=28度. 如图,△ABC是等腰直角三角形,∠C=90°,点D是AB的中点,点P是AB上的一个动点(点P与点A、B不重合),矩形PECF的顶点E,F分别在BC,AC上.
如图,△ABC是等腰直角三角形,∠C=90°,点D是AB的中点,点P是AB上的一个动点(点P与点A、B不重合),矩形PECF的顶点E,F分别在BC,AC上. 如图,在Rt△ABC中,∠A=90°,BD平分∠ABC交AC于D点,AB=4,BD=5,点P是线段BC上的一动点,则PD的最小值是3.
如图,在Rt△ABC中,∠A=90°,BD平分∠ABC交AC于D点,AB=4,BD=5,点P是线段BC上的一动点,则PD的最小值是3.