题目内容
14.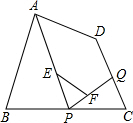 如图,在四边形ABCD中,Q是CD上的一定点,P是BC上的一动点,点E、F分别是PA、PQ的中点,当点P在BC上移动时,线段EF的长度( )
如图,在四边形ABCD中,Q是CD上的一定点,P是BC上的一动点,点E、F分别是PA、PQ的中点,当点P在BC上移动时,线段EF的长度( )| A. | 先变大,后变小 | B. | 保持不变 | C. | 先变小,后变大 | D. | 无法确定 |
分析 连接AQ,则可知EF为△PAQ的中位线,可知EF=$\frac{1}{2}$AQ,可知EF不变.
解答 解:如图,连接AQ,
∵E、F分别为PA、PQ的中点,
∴EF为△PAQ的中位线,
∴EF=$\frac{1}{2}$AQ,
∵Q为定点,
∴AQ的长不变,
∴EF的长不变,
故选B.
点评 本题主要考查三角形中位线定理,掌握三角形中位线平行第三边且等于第三边的一半是解题的关键.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
4.△ABC中,∠A,∠B,∠C所对的边分别是a,b,c,满足下列条件的△ABC,不是直角三角形的是( )
| A. | a:b:c=1:$\sqrt{2}$:1 | B. | ∠A:∠B:∠C=3:4:5 | C. | (a+b)(a-b)=c2 | D. | ∠A:∠B:∠C=1:2:3 |
5.为了了解2014年我市参加中考的334000名学生的视力情况,从中抽查了1000名学生的视力情况进行统计分析,下面判断正确的是( )
| A. | 334000名学生是总体 | |
| B. | 每名学生是总体的一个个体 | |
| C. | 1000名学生的视力情况是总体的一个样本 | |
| D. | 上述调查是普查 |
2.观察如图图形,图(1)中有3个三角形,图(2)中有5个三角形,图(3)中有7个三角形,…若依此规律下去,则第2014个图形中三角形的个数是( )


| A. | 4028 | B. | 4029 | C. | 4030 | D. | 4031 |
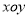 中,已知点
中,已知点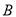 (-3,4)关于
(-3,4)关于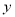 轴的对称点为
轴的对称点为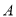 .
. 点的坐标;
点的坐标;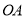 的长;
的长;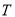 (
(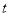 ,0)是
,0)是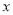 轴正半轴上的一个动点,当△ATO是等腰三角形时,求
轴正半轴上的一个动点,当△ATO是等腰三角形时,求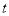 的值.
的值. .
. B.
B. C.
C. D.
D.
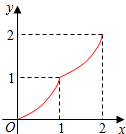
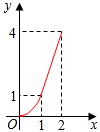
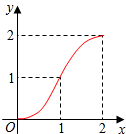
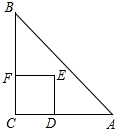 如图,Rt△ABC中,∠C=90°,AC=BC=2,正方形CDEF的顶点D、F分别在AB、BC边上,设CD的长度为x,△ABC与正方形CDEF重叠部分的面积为y,则下列图象能表示y与x之间的函数关系的是( )
如图,Rt△ABC中,∠C=90°,AC=BC=2,正方形CDEF的顶点D、F分别在AB、BC边上,设CD的长度为x,△ABC与正方形CDEF重叠部分的面积为y,则下列图象能表示y与x之间的函数关系的是( )