题目内容
如图将抛物线y=2x2向右平移a个单位长度，顶点为A，与y轴交于点B，若△AOB为等腰直角三角形，求a的值．考点：二次函数图象与几何变换
专题：
分析：先求得平移后的函数解析式，利用解析式求得点A、B的坐标，然后根据△AOB为等腰直角三角形来求a的值．
解答：解：抛物线y=2x2向右平移a个单位长度后的解析式为：y=2（x-a）2，则
A（a，0），B（0，2a2）．
∵△AOB为等腰直角三角形，
∴a=2a2，即a（1-2a）=0，
解得 a1=0（不合题意，舍去），a2=
．
即a的值是
．
A（a，0），B（0，2a2）．
∵△AOB为等腰直角三角形，
∴a=2a2，即a（1-2a）=0，
解得 a1=0（不合题意，舍去），a2=
| 1 |
| 2 |
即a的值是
| 1 |
| 2 |
点评：主要考查了函数图象的平移，抛物线与坐标轴的交点坐标的求法，要求熟练掌握平移的规律：左加右减，上加下减．并用规律求函数解析式．会利用方程求抛物线与坐标轴的交点．
练习册系列答案
相关题目
如果一个四边形的两条对角线互相垂直平分且相等，那么这个四边形是（ ）
| A、平行四边形 | B、菱形 |
| C、正方形 | D、矩形 |
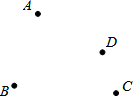点A，B，C，D的位置如图，按下列要求画出图形．
已知如图，∠BOC和∠AOC的比是3：2，OD平分∠AOB，∠COD=10°，求∠AOB的度数．
如图，⊙O是△ABC的外接圆，AF平分∠BAC交BC于点E，交⊙O于点F，BD平分∠ABC交AF于点D，过点F作FH∥BC．