题目内容
9. 如图,由四个直角边分别为3和4的全等直角三角形拼成的“赵爽弦图”,其中大正方形的面积为25.
如图,由四个直角边分别为3和4的全等直角三角形拼成的“赵爽弦图”,其中大正方形的面积为25.
分析 根据题意直接利用勾股定理得出大正方形的边长,求出面积即可.
解答 解:由题意可得:大正方形的边长为:$\sqrt{{3}^{2}+{4}^{2}}$=5,
故大正方形的面积为:25.
故答案为:25.
点评 此题主要考查了勾股定理,正确得出大正方形的边长是解题关键.

练习册系列答案
相关题目
15.用科学记数法表示的数是1.69×105,则原来的数是( )
| A. | 169 | B. | 1690 | C. | 16900 | D. | 169000 |
14.如果x=-2是方程a(x+1)=2(x-a)的解,则a等于( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{4}$ | C. | -2 | D. | -4 |
18.下列说法正确的是( )
| A. | “买一张电影票,座位号为偶数”是必然事件 | |
| B. | 若甲、乙两组数据的方差分别为s${\;}_{甲}^{2}$=0.3、s${\;}_{乙}^{2}$=0.1,则甲组数据比乙组数据稳定 | |
| C. | 一组数据2,4,5,5,3,6的众数是5 | |
| D. | 若某抽奖活动的中奖率为$\frac{1}{6}$,则参加6次抽奖一定有1次能中奖 |
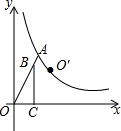 如图,点A是双曲线y=$\frac{k}{x}$(x>0)上的一点,连结OA,在线段OA上取一点B,作BC⊥x轴于点C,以BC的中点为对称中心,作点O的中心对称点O′,当O′落在这条双曲线上时,$\frac{OB}{OA}$=$\frac{\sqrt{2}}{2}$.
如图,点A是双曲线y=$\frac{k}{x}$(x>0)上的一点,连结OA,在线段OA上取一点B,作BC⊥x轴于点C,以BC的中点为对称中心,作点O的中心对称点O′,当O′落在这条双曲线上时,$\frac{OB}{OA}$=$\frac{\sqrt{2}}{2}$.