题目内容
初二(1)班有37名学生,其中参加数学竞赛的有30人,参加物理竞赛的有20人,有4人没有参加任何一项竞赛,则同时参加这两项竞赛的学生共有( )人.
| A、16 | B、17 | C、18 | D、19 |
考点:容斥原理
专题:
分析:设同时参加两项竞赛的学生有x人,根据总人数=参加数学竞赛的人数+参加物理竞赛的人数+不参加比赛的人数-两项比赛都参加的人数列出方程,求解即可.
解答:解:设同时参加两项竞赛的学生有x人,根据题意可列出方程:
37=30+20+4-x,
解得x=17(人);
故选B.
37=30+20+4-x,
解得x=17(人);
故选B.
点评:本题考查了容斥原理,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系列出方程,再求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在正九边形ABCDEFGHI中,若对角线AE=2,则AB+AC的值等于( )
A、
| ||
| B、2 | ||
C、
| ||
D、
|
气象台预报:“本市明天降水概率是80%”,但据经验,气象台预报的准确率仅为80%,则在此经验下,本市明天降水的概率为( )
| A、84% | B、80% |
| C、68% | D、64% |
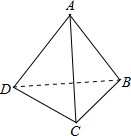 用六根火柴棒搭成4个正三角形(如图),现有一只虫子从点A出发爬行了5根不同的火柴棒后,到了C点,则不同的爬行路径共有( )
用六根火柴棒搭成4个正三角形(如图),现有一只虫子从点A出发爬行了5根不同的火柴棒后,到了C点,则不同的爬行路径共有( )| A、4条 | B、5条 | C、6条 | D、7条 |
下列各等式从左到右是因式分解的是( )
A、x-
| ||||||||
| B、x4-5x2-36=(x2+4)(x+3)(x-3) | ||||||||
| C、(5a-3)2=25a2-30a+9 | ||||||||
D、a-b=(
|
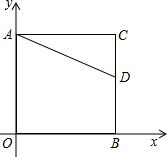 如图,正方形AOBC的B点在x轴正半轴上,A在y轴正半轴上,边长为
如图,正方形AOBC的B点在x轴正半轴上,A在y轴正半轴上,边长为