题目内容
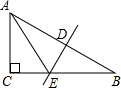
14. 如图,AD∥BC,AB⊥BC,CD⊥DE,DF⊥BC,CD=ED,AD=2,FC=1,则△ADE的面积为1.
如图,AD∥BC,AB⊥BC,CD⊥DE,DF⊥BC,CD=ED,AD=2,FC=1,则△ADE的面积为1.
分析 过E作EH⊥AD,交AD的延长线于H,证明△DEH与△DFC全等后,再利用三角形的面积解答即可.
解答 解:过E作EH⊥AD,交AD的延长线于H,如图,
∵CD⊥DE,DF⊥BC,
∴∠EDH+∠HDC=∠FDC+∠HDC=90°,
∴∠EDH=∠FDC,
在△DEH与△DFC中,
$\left\{\begin{array}{l}{∠EHD=∠CFD=90°}\\{∠EDH=∠CDF}\\{DC=DE}\end{array}\right.$,
∴△DEH≌△DFC(AAS),
∴EH=CF=1,
∴△ADE的面积=$\frac{1}{2}×AD×EH=\frac{1}{2}×2×1=1$,
故答案为:1.
点评 此题考查全等三角形的判定和性质,关键是证明△DEH与△DFC全等.

练习册系列答案
相关题目
14.(1)填表:
(2)由上你发现了什么规律?用语言叙述这个规律.
| a | 0.0001 | 0.01 | 1 | 100 | 10000 |
| $\sqrt{a}$ | 0.01 | 0.1 | 1 | 10 | 100 |
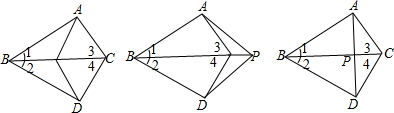
3. 如图,在Rt△ABC中,∠C=90°,斜边AB的垂直平分线DE交AB于点D,交BC于点E,且AE平分∠BAC,下列关系式不成立的是( )
如图,在Rt△ABC中,∠C=90°,斜边AB的垂直平分线DE交AB于点D,交BC于点E,且AE平分∠BAC,下列关系式不成立的是( )
 如图,在Rt△ABC中,∠C=90°,斜边AB的垂直平分线DE交AB于点D,交BC于点E,且AE平分∠BAC,下列关系式不成立的是( )
如图,在Rt△ABC中,∠C=90°,斜边AB的垂直平分线DE交AB于点D,交BC于点E,且AE平分∠BAC,下列关系式不成立的是( )| A. | AC=2EC | B. | ∠B=∠CAE | C. | ∠DEA=∠CEA | D. | BC=3CE |

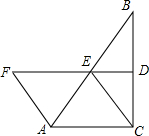 如图,AC的垂线BC与菱形ACEF的对角线AE的延长线交于点B,FE的延长线交BC于点D.
如图,AC的垂线BC与菱形ACEF的对角线AE的延长线交于点B,FE的延长线交BC于点D.