题目内容
 如图,利用一面长为18米的墙,用36米篱笆围成一个矩形场地ABCD,设AD长为x米,AB长为y米,且x<y,矩形的面积为S平方米.
如图,利用一面长为18米的墙,用36米篱笆围成一个矩形场地ABCD,设AD长为x米,AB长为y米,且x<y,矩形的面积为S平方米.(1)求y与x的函数关系式,并直接写出自变量x的取值范围;
(2)求S与x的函数关系式,并求出使矩形场地的面积为160平方米的围法.
考点:二次函数的应用,一元二次方程的应用
专题:几何图形问题
分析:(1)由图可知AB=(篱笆长-2AD),把相关数值代入即可求解;
(2)等量关系为:AB×AD=160,把相关数值代入即可求解.
(2)等量关系为:AB×AD=160,把相关数值代入即可求解.
解答:解:(1)∵AD=BC=xm,
∴AB=36-2xm,
由题意得y=x(36-2x),
=-2x2+36x(9≤x<12).
(2)当S=160时得:
S=-2x2+80x=160,
解得:x1=10,x2=8
∵9≤x<12,
∴x=8(舍去),
∴AD=10m.
∴AB=36-2xm,
由题意得y=x(36-2x),
=-2x2+36x(9≤x<12).
(2)当S=160时得:
S=-2x2+80x=160,
解得:x1=10,x2=8
∵9≤x<12,
∴x=8(舍去),
∴AD=10m.
点评:此题考查了二次函数的应用,不仅是一道实际问题,而且结合了矩形的性质,解答此题要注意以下问题:(1)矩形的一边为墙,且墙的长度不超过18米;(2)根据矩形的面积公式列一元二次方程并根据根的判别式来判断是否两边长相等.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,已知l1∥l2,点E,F在l1上,点G,H在l2上,试说明△EGO与△FHO面积相等.
如图,已知l1∥l2,点E,F在l1上,点G,H在l2上,试说明△EGO与△FHO面积相等.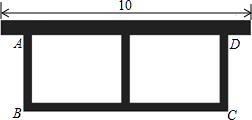 如图,园艺工人利用长24m的篱笆,一面利用墙(墙的最大长度为10m),围成中间隔有一道篱笆的长方形花圃,用以种植红玫瑰和蓝玫瑰.设花圃的边AB长为xm,BC边长为ym.
如图,园艺工人利用长24m的篱笆,一面利用墙(墙的最大长度为10m),围成中间隔有一道篱笆的长方形花圃,用以种植红玫瑰和蓝玫瑰.设花圃的边AB长为xm,BC边长为ym. 如图,抛物线
如图,抛物线 如图,△AOB中,∠AOB=90°,AO=3,BO=6,△AOB绕顶点O逆时针旋转到△A′OB′处,此时线段A′B′与BO的交点E为BO的中点.
如图,△AOB中,∠AOB=90°,AO=3,BO=6,△AOB绕顶点O逆时针旋转到△A′OB′处,此时线段A′B′与BO的交点E为BO的中点. 如图,点B是△ADC的边AD的延长线上一点,若∠C=50°,∠BDE=60°,∠ADC=70°.求证:DE∥AC.
如图,点B是△ADC的边AD的延长线上一点,若∠C=50°,∠BDE=60°,∠ADC=70°.求证:DE∥AC.