题目内容
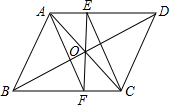 如图所示,在平行四边形ABCD中,O是对角线AC和BD的交点,过O作EF⊥AD于E,交BC于F,连结AF和CE.试说明:四边形AFCE是平行四边形.
如图所示,在平行四边形ABCD中,O是对角线AC和BD的交点,过O作EF⊥AD于E,交BC于F,连结AF和CE.试说明:四边形AFCE是平行四边形.考点:平行四边形的判定与性质
专题:证明题
分析:利用全等三角形的判定定理AAS证得△AOE≌△COF,则AE=CF,结合已知条件,由“一组对边平行且相等的四边形为平行四边形”证得结论.
解答: 证明:如图,∵四边形ABCD是平行四边形,
证明:如图,∵四边形ABCD是平行四边形,
∴AO=CO,AD∥BC,则AE∥FC.
又∵EF⊥AD,
∴EF⊥BC,
∴∠AEO=∠CFO=90°,
在△AOE与△COF中,
,
∴△AOE≌△COF(AAS),
∴AE=CF,
∴四边形AFCE是平行四边形.
 证明:如图,∵四边形ABCD是平行四边形,
证明:如图,∵四边形ABCD是平行四边形,∴AO=CO,AD∥BC,则AE∥FC.
又∵EF⊥AD,
∴EF⊥BC,
∴∠AEO=∠CFO=90°,
在△AOE与△COF中,
|
∴△AOE≌△COF(AAS),
∴AE=CF,
∴四边形AFCE是平行四边形.
点评:本题考查了平行四边形的判定与性质.平行四边形的判定方法共有五种,应用时要认真领会它们之间的联系与区别,同时要根据条件合理、灵活地选择方法.

练习册系列答案
相关题目
数据1、2、5、3、5、3、5的众数是( )
| A、1 | B、2 | C、3 | D、5 |
 如图,点D在Rt△ABC的斜边AB上,AD=7,DB=11,∠CDB=2∠B,则CD=
如图,点D在Rt△ABC的斜边AB上,AD=7,DB=11,∠CDB=2∠B,则CD=