题目内容
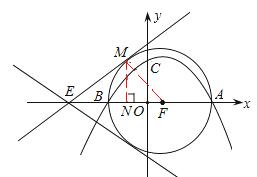
如图,抛物线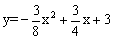 与x轴交于A、B两点(点A在点B的右侧),与y轴交于点C。若直线l过点E(﹣4,0),M为直线l上的动点
与x轴交于A、B两点(点A在点B的右侧),与y轴交于点C。若直线l过点E(﹣4,0),M为直线l上的动点 ,当以A、B、M为顶点所作的直角三角形有且只有三个时,求直线l的解析式.
,当以A、B、M为顶点所作的直角三角形有且只有三个时,求直线l的解析式.
解:在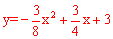 中,令y=0,即
中,令y=0,即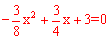 ,解得x1=﹣2,x2=4。
,解得x1=﹣2,x2=4。
∵点A在点B的右侧,
∴A、B点的坐标为A(4,0)、B(﹣2,0)。
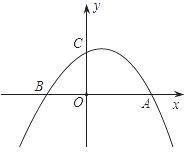
如图,以AB为直径作⊙F,圆心为F.过E点作⊙F的切线,这样的切线有2条,连接FM,过M作MN⊥x轴于点N。

 则ON=
则ON=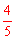 。
。
∴M点坐标为(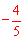 ,
,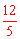 )。
)。
直线l过M(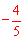 ,
,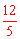 ),E(﹣4,0),
),E(﹣4,0),
设直线l的解析式为y=k1x+b1,则有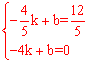 ,解得
,解得 。
。
∴直线l的解析式为y= x+3。
x+3。
同理,可以求得另一条 切线的解析式为y=
切线的解析式为y=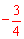 x﹣3。
x﹣3。
综上所述,直线l的 解析式为y=
解析式为y= x+3或y=
x+3或y=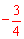 x﹣3。
x﹣3。
【考点】二次函数综合题 ,待定系数法,曲线上点的坐标与方程的关系,二次函数的性质,勾股定理,直线与圆的位置关系,直线与圆相切的性
,待定系数法,曲线上点的坐标与方程的关系,二次函数的性质,勾股定理,直线与圆的位置关系,直线与圆相切的性 质,圆周角定理,锐角三角函数定义,分类思想的应用。
质,圆周角定理,锐角三角函数定义,分类思想的应用。


练习册系列答案
相关题目
 BCD,其中AB=
BCD,其中AB= 2,AD=1,将矩形ABCD沿x轴的正方向无滑动的在x轴上滚动,当点A离开原点后第一次落在x轴上时,点A运动的路径线与x轴围成的面积为
2,AD=1,将矩形ABCD沿x轴的正方向无滑动的在x轴上滚动,当点A离开原点后第一次落在x轴上时,点A运动的路径线与x轴围成的面积为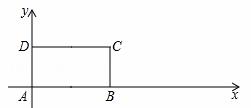
 B以1cm/s的速度运动,点P、Q分别从A、C同时出发,设运动时间为t (s).
B以1cm/s的速度运动,点P、Q分别从A、C同时出发,设运动时间为t (s). 边能构成一个三角形;②当t为何值时,四边形PQCD为等腰梯形.
边能构成一个三角形;②当t为何值时,四边形PQCD为等腰梯形. 动.当t为何值时,以P、Q、C、D为顶点的四边形是平行四边形.
动.当t为何值时,以P、Q、C、D为顶点的四边形是平行四边形.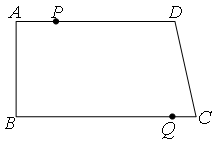

 、F、G、H分别在NP、PQ、QM、MN上,若
、F、G、H分别在NP、PQ、QM、MN上,若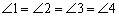
 ,则称四边形EF
,则称四边形EF GH为矩形MNPQ的反射四边形.在图2、图3中,四边形ABCD为矩形,且
GH为矩形MNPQ的反射四边形.在图2、图3中,四边形ABCD为矩形,且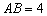
 ,
,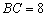
 .
.
 2中的四边形EFGH是利用正方形网格在图上画出的矩形ABCD的反射四边形.请你利用正方形网格在图3上画出矩形ABCD的反射四边形EFGH;
2中的四边形EFGH是利用正方形网格在图上画出的矩形ABCD的反射四边形.请你利用正方形网格在图3上画出矩形ABCD的反射四边形EFGH; 值,请直接写出图2、图3中矩形ABCD的反射四边形E
值,请直接写出图2、图3中矩形ABCD的反射四边形E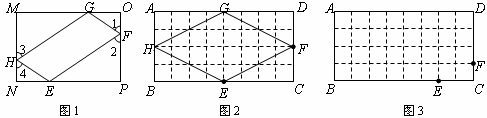

 度,沿射线AB作匀速运动。当P运动到C点时,P、Q都停止运动
度,沿射线AB作匀速运动。当P运动到C点时,P、Q都停止运动 。设点P运动的时间为ts。
。设点P运动的时间为ts。
 为
为 边BC上的一点,AE⊥DE,AB=12,BE=
边BC上的一点,AE⊥DE,AB=12,BE=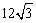 ,F为线段BE上一点,EF=7,连接AF。如图1,现有一张硬纸片△GMN,∠NGM=900,NG=6,MG=
,F为线段BE上一点,EF=7,连接AF。如图1,现有一张硬纸片△GMN,∠NGM=900,NG=6,MG=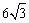 ,斜边MN与边BC在同一直线上,点N与点E重合,点G在线段DE上。如图2,△GMN从图1的位置出发,以每秒1个单位的速度沿EB向点B匀速移动,同时,点P从A点
,斜边MN与边BC在同一直线上,点N与点E重合,点G在线段DE上。如图2,△GMN从图1的位置出发,以每秒1个单位的速度沿EB向点B匀速移动,同时,点P从A点 出发,以每秒2个单位的速度沿AD向点D匀速移动,点Q为直线GN与线段AE的交点,连接PQ。当点G到达线段AE上时,△GMN和点P同时停止运动。设运动时间为t秒,解答问题:
出发,以每秒2个单位的速度沿AD向点D匀速移动,点Q为直线GN与线段AE的交点,连接PQ。当点G到达线段AE上时,△GMN和点P同时停止运动。设运动时间为t秒,解答问题: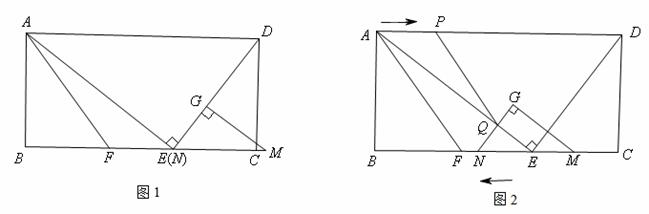
 时,
时,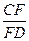 的值为( )
的值为( )

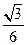 C.
C.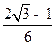
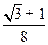
 ,
, 。
。 。
。