题目内容
18.化简$\frac{a}{{a}^{2}-4}$•$\frac{a+2}{{a}^{2}-3a}$-$\frac{1}{2-a}$,并求值,其中a与2、3构成△ABC的三边,且a为整数.分析 原式第一项约分后,两项通分并利用同分母分式的减法法则计算得到最简结果,把a的值代入计算即可求出值.
解答 解:原式=$\frac{a}{(a+2)(a-2)}$•$\frac{a+2}{a(a-3)}$+$\frac{1}{a-2}$=$\frac{1}{(a-2)(a-3)}$+$\frac{1}{a-2}$=$\frac{1+a-3}{(a-2)(a-3)}$=$\frac{a-2}{(a-2)(a-3)}$=$\frac{1}{a-3}$,
∵a与2、3构成△ABC的三边,且a为整数,
∴1<a<5,即a=2,3,4,
当a=2或a=3时,原式没有意义,
则a=4时,原式=1.
点评 此题考查了分式的化简求值,以及三角形三边关系,熟练掌握运算法则是解本题的关键.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
9.一组数据2,6,5,2,4,则这组数据的中位数是( )
| A. | 2 | B. | 4 | C. | 5 | D. | 6 |
13.下列运算正确的是( )
| A. | a•a2=a2 | B. | (a2)3=a6 | C. | a2+a3=a6 | D. | a6÷a2=a3 |
7.化简$\frac{{m}^{2}}{m-3}$-$\frac{9}{m-3}$的结果是( )
| A. | m+3 | B. | m-3 | C. | $\frac{m-3}{m+3}$ | D. | $\frac{m+3}{m-3}$ |
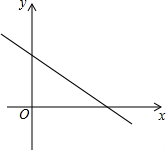 如图,直线l经过点A(4,0),B(0,3).
如图,直线l经过点A(4,0),B(0,3). 如图,在△A1B1C1中,已知A1B1=7,B1C1=4,A1C1=5,依次连接△A1B1C1三边中点,得△A2B2C2,再依次连接△A2B2C2的三边中点得△A3B3C3,…,则△A5B5C5的周长为1.
如图,在△A1B1C1中,已知A1B1=7,B1C1=4,A1C1=5,依次连接△A1B1C1三边中点,得△A2B2C2,再依次连接△A2B2C2的三边中点得△A3B3C3,…,则△A5B5C5的周长为1. 数学活动课上,四位同学围绕作图问题:“如图,已知直线l和l外一点P,用直尺和圆规作直线PQ,使PQ⊥l于点Q.”分别作出了下列四个图形.其中作法错误的是( )
数学活动课上,四位同学围绕作图问题:“如图,已知直线l和l外一点P,用直尺和圆规作直线PQ,使PQ⊥l于点Q.”分别作出了下列四个图形.其中作法错误的是( )


