题目内容
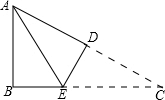 如图,Rt△ABC中,∠B=90°,AB=3cm,AC=5cm,将△ABC折叠,使点C与点A重合,折痕为DE,则CE=
如图,Rt△ABC中,∠B=90°,AB=3cm,AC=5cm,将△ABC折叠,使点C与点A重合,折痕为DE,则CE=考点:翻折变换(折叠问题)
专题:
分析:先根据勾股定理求出BC的值,再由轴对称的性质和勾股定理的性质就可以求出CE的值.
解答:解:∵∠B=90°,AB=3cm,AC=5cm,由勾股定理,得
∴BC=4.
∵△ADE与△CDE关于DE对称,
∴△ADE≌△CDE,
∴AE=CE,AD=CD=2.5cm.
设CE=x,则BE=4-x,AE=x,由勾股定理,得
9+(4-x)2=x2.
解得:x=
故答案为:
.
∴BC=4.
∵△ADE与△CDE关于DE对称,
∴△ADE≌△CDE,
∴AE=CE,AD=CD=2.5cm.
设CE=x,则BE=4-x,AE=x,由勾股定理,得
9+(4-x)2=x2.
解得:x=
| 25 |
| 8 |
故答案为:
| 25 |
| 8 |
点评:本题考查了勾股定理的运用,轴对称的性质的运用,解答时根据轴对称的性质求解是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列选项中是同类项的是( )
A、-2a与
| ||
| B、-2a2b与a2b | ||
| C、2m与2n | ||
D、-xy2与
|
已知方程x2-5x+2=0的两根分别是x1,x2,则x1-x1x2+x2的值为( )
| A、-7 | B、-3 | C、7 | D、3 |
 如图,在△ABC中,AD为△ABC的边BC上的中线,E、F分别是AB、AC上的点,且EF∥BC,AD与EF相交于点O,求证:OF=OE.
如图,在△ABC中,AD为△ABC的边BC上的中线,E、F分别是AB、AC上的点,且EF∥BC,AD与EF相交于点O,求证:OF=OE. 如图,是二次函数y=ax2+bx+c的图象的一部分,其对称轴是直线x=1,且过点(4,1),则满足函数y≤1的x的取值范围是
如图,是二次函数y=ax2+bx+c的图象的一部分,其对称轴是直线x=1,且过点(4,1),则满足函数y≤1的x的取值范围是