题目内容
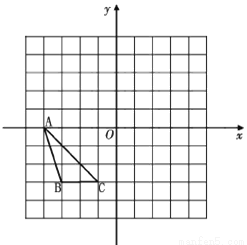
如图,在边长为1的正方形网格中,△ABC的顶点均在格点上.
(1)画出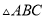 关于原点成中心对称的△A′B′C′,并直接写出△A′B′C′各顶点的坐标.
关于原点成中心对称的△A′B′C′,并直接写出△A′B′C′各顶点的坐标.
(2)求点B旋转到点B′的路径(结果保留π).
练习册系列答案
 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
题目内容
如图,在边长为1的正方形网格中,△ABC的顶点均在格点上.
(1)画出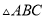 关于原点成中心对称的△A′B′C′,并直接写出△A′B′C′各顶点的坐标.
关于原点成中心对称的△A′B′C′,并直接写出△A′B′C′各顶点的坐标.
(2)求点B旋转到点B′的路径(结果保留π).

 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案