Question

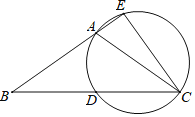
【题目】如图，在△ABC中，AB＝AC，D是BC边上的中点，过A，C，D三点的圆交BA的延长线于点E，连接EC．

（1）求证：∠E＝90°；

（2）若AB＝6，BC＝10，求AE的长．

Answer 1

【答案】（1）见解析；（2）

【解析】

（1）连接AD，根据等腰三角形“三线合一”的性质知∠ADC＝∠ADB＝90°，从而知点A，C，D在以AC为直径的圆上，再根据圆周角定理可得答案；

（2）证△BAD∽△BCE得＝，将有关线段长度代入计算可得．

解：（1）如图，连接AD，

∵AB＝AC，D是BC中点，

∴AD⊥BC，即∠ADC＝∠ADB＝90°，

∴点A，C，D在以AC为直径的圆上，

∴∠E＝90°；

（2）∵BC＝10，

∴BD＝BC＝5，

∵∠B＝∠B，∠ADB＝∠E＝90°，

∴△BAD∽△BCE，

∴＝，即＝，

解得：AE＝．