题目内容
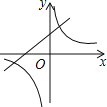
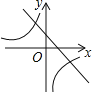
【题目】如图,在平面直角坐标系xOy中,B(3,﹣1)是反比函数y=![]() 图象上的一点,过B点的一次函数y=﹣x+b与反比例函数交于另一点A.
图象上的一点,过B点的一次函数y=﹣x+b与反比例函数交于另一点A.
(1)求一次函数和反比例函数的表达式;
(2)求△AOB面积;
(3)在A点左边的反比例函数图象上求点P,使得S△POA:S△AOB=3:2.

【答案】(1)y=﹣x+2;y=﹣![]() ;(2)S△AOB=4;(3)P(﹣2﹣
;(2)S△AOB=4;(3)P(﹣2﹣![]() ,3
,3![]() ﹣6).
﹣6).
【解析】
(1)根据已知点的坐标求出函数解析式(2)先求A点和C点的坐标,再根据三角形的面积公式计算面积(3)先做辅助线,再设点P坐标,列出一元二次方程解方程即可得到结果.
解:(1)∵一次函数y=﹣x+b过B(3,﹣1),
∴﹣3+b=﹣1,b=2,
∴一次函数表达式为y=﹣x+2;
∵B(3,﹣1)是反比函数y=![]() 图象上的一点,
图象上的一点,
∴k=3×(﹣1)=﹣3,
∴反比例函数的表达式为![]() ;
;
(2)由 ,解得
,解得![]() 或
或![]() ,
,
∴A(﹣1,3).
如图,设直线y=﹣x+2与y轴交于点C,则C(0,2),
∴S△AOB=S△AOC+S△COB
=![]() ×2×1+
×2×1+![]() ×2×3
×2×3
=1+3
=4;
(3)如图,过点A作AM⊥x轴于点M,过点P作PN⊥x轴于点N,

则S△AOM=S△PON=![]() .
.
∵S△POA+S△PON=S梯形AMNP+S△AOM,
∴S△POA=S梯形AMNP,
∵S△POA:S△AOB=3:2,
∴S△POA=![]() S△AOB=
S△AOB=![]() ×4=6.
×4=6.
设P(x,﹣![]() ),而A(﹣1,3),
),而A(﹣1,3),
∴S梯形AMNP=![]() (NP+AM)MN=6,
(NP+AM)MN=6,
∴![]() (﹣
(﹣![]() +3)(﹣1﹣x)=6,
+3)(﹣1﹣x)=6,
整理,得x2+4x﹣1=0,
解得x=﹣2±![]() ,
,
∵点P在A点左边,
∴x<﹣1,
∴x=﹣2﹣![]() ,
,
∴P(﹣2﹣![]() ,3
,3![]() ﹣6).
﹣6).

练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目