Question

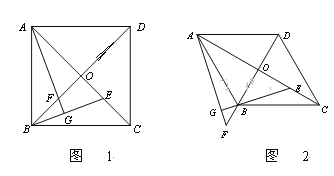
【题目】在四边形ABCD中，对角线AC与BD交于点O，E是OC上任意一点，AG⊥BE于点G，交BD于点F．

（1）如图1,若四边形ABCD是正方形,

①求证：△AOF≌△BOE；

②连接EF,判断EF与BC的位置关系，并说明理由。

（2）如图2,若四边形ABCD是菱形, ∠ABC=1200，求的值.

Answer 1

【答案】（1）①证明见解析②EF∥BC（2）

【解析】分析：(1)、根据正方形的性质得出AO=BO，根据AG⊥BE得出∠AEG=∠AFO，从而得出三角形全等；(2)、根据全等得出OE=OF，从而得出∠OEF=∠OFE=45°，从而得出平行线；根据菱形的性质得出△AOF和△BOE相似，从而得出，然后根据直角三角形的性质得出答案．

详解：（1）①证明：∵四边形ABCD是正方形，∴AO=BO, ，∴∠AOF=∠BOE=900，

∴∠AFO+∠FAO=900，∵，∴∠AEG+∠GAE=900，∴∠AEG=∠AFO，∴△≌△；

②EF∥BC，理由如下：

由①得△≌△， ∴OE=OF， ∴∠OEF=∠OFE=450，∴∠OEF=∠OBC，∴EF∥BC ；

（2） ∵四边形是菱形，， ∴,，

∴， ∵，∴， ∴，

又∵， ∴，∴，

∵，，∴， ∴．