题目内容
9．若方程组$\left\{\begin{array}{l}{3x+y=2+3a}\\{x+3y=2+a}\end{array}\right.$的解满足x+y＞0，则a的取值范围是（ ）| A． | a＜-1 | B． | a＜1 | C． | a＞-1 | D． | a＞1 |
分析 方程组中的两个方程相加，即可求出x+y=1+a，根据已知得出不等式，求出不等式的解集即可．
解答 解：$\left\{\begin{array}{l}{3x+y=2+3a①}\\{x+3y=2+a②}\end{array}\right.$
①+②得：4x+4y=4+4a，
即x+y=1+a，
∵x+y＞0，
∴1+a＞0，
∴a＞-1，
故选C．
点评 本题考查了二元一次方程组的解，解一元一次不等式的应用，能求出关于a的不等式是解此题的关键．
练习册系列答案
相关题目
17．下列计算正确的是（ ）
| A． | a2•a3=a6 | B． | （-a3）2=-a6 | C． | $\sqrt{2}+\sqrt{3}=\sqrt{5}$ | D． | -22-3=-7 |
如图，△ABC三个顶点都在5×5的网格（每个小正方形的边长均为1单位长度）的格点上，将△ABC绕点C顺时针旋转到△A′B′C的位置，且A′、B′仍落在格点上，求线段AC扫过的扇形所围成的圆锥体的底面半径．
14．
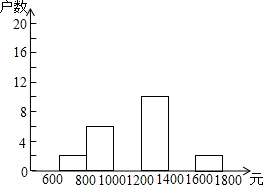小龙在学校组织的社会调查活动中负责了解他所居住的小区480户居民的家庭收入情况．他从中随机调查了40户居民家庭收入情况（收入取整数，单位：元），并绘制了如下的频数分布表和频数分布直方图．
根据以上提供的信息，解答下列问题：
（1）补全频数分布表．
（2）补全频数分布直方图．
（3）请你估计该居民小区家庭属于中等收入（大于1000不足1600元）的大约有多少户？
小龙在学校组织的社会调查活动中负责了解他所居住的小区480户居民的家庭收入情况．他从中随机调查了40户居民家庭收入情况（收入取整数，单位：元），并绘制了如下的频数分布表和频数分布直方图．| 分组 | 频数 | 百分比 |
| 600≤x＜800 | 2 | 5% |
| 800≤x＜1000 | 6 | 15% |
| 1000≤x＜1200 | a | 45% |
| 1200≤x＜1400 | 9 | 22.5% |
| 1400≤x＜1600 | b | c |
| 1600≤x＜1800 | 2 | d |
| 合计 | 40 | 100% |
（1）补全频数分布表．
（2）补全频数分布直方图．
（3）请你估计该居民小区家庭属于中等收入（大于1000不足1600元）的大约有多少户？
1．下列函数中，不属于二次函数的是（ ）
| A． | y=（x-2）2 | B． | y=-2（x+1）（x-1） | C． | y=1-x-x2 | D． | y=$\frac{1}{{x}^{2}-1}$ |
18．在△ABC中，AB=AC，∠B的外角=100゜，那么∠A=（ ）
| A． | 10゜ | B． | 20゜ | C． | 60゜ | D． | 80゜ |