题目内容
如图,已知AB∥DC,BF平分∠ABE,CF平分∠DCE,BF与CF相交于F
(1)如图①,若∠F=30°,求∠E的度数;
(2)如图②,若设∠F=α,∠E=β,请你猜想α与β之间的关系(直接写出结果不用说明理由);
(3)在图③中,(2)中α与β之间的关系是否仍然成立?若成立说明理由,若不成立写出它们之间的关系,并说明理由.
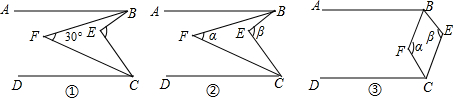
(1)如图①,若∠F=30°,求∠E的度数;
(2)如图②,若设∠F=α,∠E=β,请你猜想α与β之间的关系(直接写出结果不用说明理由);
(3)在图③中,(2)中α与β之间的关系是否仍然成立?若成立说明理由,若不成立写出它们之间的关系,并说明理由.

考点:平行线的性质
专题:
分析:(1)过点F作FM∥AB,过点E作EN∥AB,根据AB∥DC可知FM∥CD,EN∥CD,故可得出∠1=∠3,∠2=∠4.∠ABE=∠5,∠DCE=∠6,再由BF平分∠ABE,CF平分∠DCE,可知∠1=
∠5,∠2=
∠6,由此即可得出结论;
(2)同(1)即可得出结论;
(3)过点F作FM∥AB,根据AB∥DC,可知FM∥CD,故∠1=∠3,∠2=∠4,再由BF平分∠ABE,CF平分∠DCE可得出∠EBF=∠1=∠3,∠ECF=∠2=∠4,根据四边形内角和定理可知α+β+(∠EBF+∠ECF)=360°,故可得出结论.
| 1 |
| 2 |
| 1 |
| 2 |
(2)同(1)即可得出结论;
(3)过点F作FM∥AB,根据AB∥DC,可知FM∥CD,故∠1=∠3,∠2=∠4,再由BF平分∠ABE,CF平分∠DCE可得出∠EBF=∠1=∠3,∠ECF=∠2=∠4,根据四边形内角和定理可知α+β+(∠EBF+∠ECF)=360°,故可得出结论.
解答: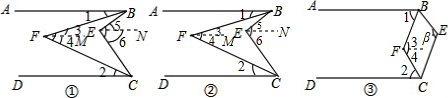 解:(1)如图①过点F作FM∥AB,过点E作EN∥AB.
解:(1)如图①过点F作FM∥AB,过点E作EN∥AB.
∵AB∥DC,
∴FM∥CD,EN∥CD,
∴∠1=∠3,∠2=∠4.∠ABE=∠5,∠DCE=∠6
∵BF平分∠ABE,CF平分∠DCE,
∴∠1=
∠5,∠2=
∠6,
∴∠3+∠4=∠1+∠2=
(∠5+∠6),即∠BFC=
∠BEC.
∵∠BFC=30°,
∴∠BEC=60°;
(2)β=2α.
理由:如图②,过点F作FM∥AB,过点E作EN∥AB.
同(1)可得∠BFC=
∠BEC,
∵∠BFC=α,
∴∠BEC=2∠BFC=2α,即β=2α;
(3)不成立.
如图③,过点F作FM∥AB,
∵AB∥DC,
∴FM∥CD,
∴∠1=∠3,∠2=∠4,
∵BF平分∠ABE,CF平分∠DCE,
∴∠EBF=∠1=∠3,∠ECF=∠2=∠4,
∴∠EBF+∠ECF=∠1+∠2=α,
∵α+β+(∠EBF+∠ECF)=360°,
∴α+β+α=360°,即2α+β=360°.
 解:(1)如图①过点F作FM∥AB,过点E作EN∥AB.
解:(1)如图①过点F作FM∥AB,过点E作EN∥AB.∵AB∥DC,
∴FM∥CD,EN∥CD,
∴∠1=∠3,∠2=∠4.∠ABE=∠5,∠DCE=∠6
∵BF平分∠ABE,CF平分∠DCE,
∴∠1=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠3+∠4=∠1+∠2=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠BFC=30°,
∴∠BEC=60°;
(2)β=2α.
理由:如图②,过点F作FM∥AB,过点E作EN∥AB.
同(1)可得∠BFC=
| 1 |
| 2 |
∵∠BFC=α,
∴∠BEC=2∠BFC=2α,即β=2α;
(3)不成立.
如图③,过点F作FM∥AB,
∵AB∥DC,
∴FM∥CD,
∴∠1=∠3,∠2=∠4,
∵BF平分∠ABE,CF平分∠DCE,
∴∠EBF=∠1=∠3,∠ECF=∠2=∠4,
∴∠EBF+∠ECF=∠1+∠2=α,
∵α+β+(∠EBF+∠ECF)=360°,
∴α+β+α=360°,即2α+β=360°.
点评:本题考查的是平行线的性质及角平分线的定义,根据题意作出辅助线,构造出平行线是解答此题的关键.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
 如图,直线AB与x轴交于点A(1,0),与y轴交于点B(0,-2).
如图,直线AB与x轴交于点A(1,0),与y轴交于点B(0,-2). 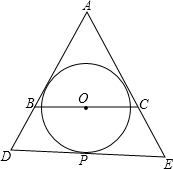 如图,△ABC中,AB=AC,BC=6,O是BC的中点,圆O与两腰相切,动点P在圆O上,过点P的圆O切线分别和AB,AC的延长线相交于点D,E. BD•CE的值是常量吗?若是常量,请求之;若不是,请说明理由.
如图,△ABC中,AB=AC,BC=6,O是BC的中点,圆O与两腰相切,动点P在圆O上,过点P的圆O切线分别和AB,AC的延长线相交于点D,E. BD•CE的值是常量吗?若是常量,请求之;若不是,请说明理由. 如图,已知直线m∥n,直角三角板ABC的顶点A在直线m上,则∠α=
如图,已知直线m∥n,直角三角板ABC的顶点A在直线m上,则∠α=