题目内容
12.若关于x,y的方程组$\left\{\begin{array}{l}{x+y=5k+2}\\{x-y=4k-5}\end{array}\right.$的解满足x<0、y>0,求k应满足的条件.分析 将k看做已知数解方程组可得x=$\frac{9k-3}{2}$、y=$\frac{k+7}{2}$,根据x<0、y>0可得关于k的不等式组,解之可得.
解答 解:将方程组中两方程相加可得:2x=9k-3,
∴x=$\frac{9k-3}{2}$,
两方程相减可得2y=k+7,
∴y=$\frac{k+7}{2}$,
∵x<0、y>0,
∴$\left\{\begin{array}{l}{\frac{9k-3}{2}<0}\\{\frac{k+7}{2}>0}\end{array}\right.$,
解得:-7<k<$\frac{1}{3}$.
点评 本题主要考查解方程组和不等式组的能力,根据题意列出关于k的不等式组是解题的关键.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
 作出与线段AB关于y轴对称的线段A′B′.
作出与线段AB关于y轴对称的线段A′B′.
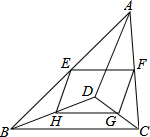 如图,D是△ABC内一点,E、F、G、H分别是AB、AC、CD、BD的中点,求证:四边形EFGH是平行四边形.
如图,D是△ABC内一点,E、F、G、H分别是AB、AC、CD、BD的中点,求证:四边形EFGH是平行四边形. 如图,在长方形ABCD中,AD=8cm,CD=4cm.
如图,在长方形ABCD中,AD=8cm,CD=4cm.