题目内容
14.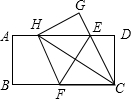 如图,在一张矩形纸片ABCD中,AB=4,BC=8,点E,F分别在AD,BC上,将纸片ABCD沿直线EF折叠,点C落在AD上的一点H处,点D落在点G处,则线段BF的取值范围为3≤BF≤4.
如图,在一张矩形纸片ABCD中,AB=4,BC=8,点E,F分别在AD,BC上,将纸片ABCD沿直线EF折叠,点C落在AD上的一点H处,点D落在点G处,则线段BF的取值范围为3≤BF≤4.
分析 如图1、2,在点H或点E的极限位置处,作出符合题意的两个几何图形;在图1中,由题意得AF=CF(设为λ),运用勾股定理列出关于λ的方程,求出λ,进而得到BF的值.在图2中,首先证明∠CEF=∠CFE,得到CF=CE=4,进而求出BF的值.
解答 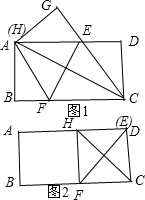 解:如图1,当点H与点A重合时,
解:如图1,当点H与点A重合时,
∵四边形ABCD为矩形,
∴∠B=90°;
由题意得:AF=CF(设为λ),则BF=8-λ;
由勾股定理得:λ2=42+(8-λ)2,
解得:λ=5,BF=3;
如图2,当点E与点D重合时,
由翻折变换的性质得:∠HEF=∠CEF=45°,HE=CE;
∴∠CEF=∠CFE,
∴CF=CE=4,BF=8-4=4,
综上所述,线段BF的取值范围为3≤BF≤4.
故答案为3≤BF≤4.
点评 该题主要考查了翻折变换的性质、矩形的性质、勾股定理等几何知识点及其应用问题;解题的关键是深入把握题意,运用分类讨论的数学思想,正确作出符合题意的几何图形,根据图形逐一解析.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
9.下列命题中是假命题的是( )
| A. | 垂直于弦的直径平分弦 | |
| B. | 若a>b,c>0,则ac>bc | |
| C. | 反比例函数y=$\frac{k}{x}$,当k>0时,y随x的增大而减少 | |
| D. | 对角线互相平分且垂直的四边形是菱形 |
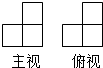 由一些相同的立方体搭成某几何体,这个几何体的主视图和俯视图如图所示,请问搭这样一个几何体最多需要多少小立方体?( )
由一些相同的立方体搭成某几何体,这个几何体的主视图和俯视图如图所示,请问搭这样一个几何体最多需要多少小立方体?( )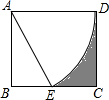 如图,矩形纸片ABCD,AD=4,以A为圆心画弧交于BC中点E,则图中围成阴影部分图形的周长为9.4.(其中π取3,$\sqrt{3}$≈1.7)
如图,矩形纸片ABCD,AD=4,以A为圆心画弧交于BC中点E,则图中围成阴影部分图形的周长为9.4.(其中π取3,$\sqrt{3}$≈1.7)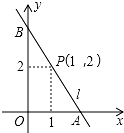 如图,直线l经过点P(1,2),与坐标轴交于A(a,0),B(0,b)两点(其中a<b,如果a+b=6,那么tan∠ABO的值为$\frac{1}{2}$.
如图,直线l经过点P(1,2),与坐标轴交于A(a,0),B(0,b)两点(其中a<b,如果a+b=6,那么tan∠ABO的值为$\frac{1}{2}$.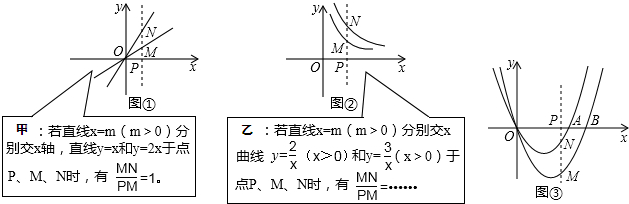
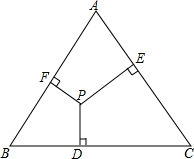 有一块等边三角形的空地,小明和小亮想在这块空地上找到一点,使得这一点到三边的距离之和最短,他们做了几次实验,发现无论三角形内的哪一点到三边的距离之和都是相等的.于是他们编了一道几何题:如图,已知点P为正△ABC内一点,点P到BC,CA,AB的距离分别为PD,PE,PF,试说明PD+PE+PF总是一个定值.这个定值与什么有关?你发现这个事实了吗?你能解出他们编的数学问题吗?
有一块等边三角形的空地,小明和小亮想在这块空地上找到一点,使得这一点到三边的距离之和最短,他们做了几次实验,发现无论三角形内的哪一点到三边的距离之和都是相等的.于是他们编了一道几何题:如图,已知点P为正△ABC内一点,点P到BC,CA,AB的距离分别为PD,PE,PF,试说明PD+PE+PF总是一个定值.这个定值与什么有关?你发现这个事实了吗?你能解出他们编的数学问题吗?