题目内容
5.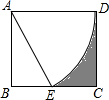 如图,矩形纸片ABCD,AD=4,以A为圆心画弧交于BC中点E,则图中围成阴影部分图形的周长为9.4.(其中π取3,$\sqrt{3}$≈1.7)
如图,矩形纸片ABCD,AD=4,以A为圆心画弧交于BC中点E,则图中围成阴影部分图形的周长为9.4.(其中π取3,$\sqrt{3}$≈1.7)
分析 根据BE=CE,求得∠BAE=30°,再根据弧长公式l=$\frac{nπr}{180}$求得弧DE的长,再计算即可.
解答 解:∵四边形ABCD为矩形,
∴AD=BC,
∵AD=4,
∴BC=4,
∵BE=CE,
∴BE=2,
∴∠BAE=30°,
∴∠DAE=60°,
∴l=$\frac{nπr}{180}$=$\frac{60π×4}{180}$=$\frac{4}{3}$π,
∴阴影部分图形的周长=$\frac{4}{3}$π+4+4=$\frac{4}{3}$π+8=$\frac{4}{3}$×1.7+8=9.4.
故答案为9.4.
点评 本题考查了弧长公式的计算以及矩形的性质,熟练运用弧长公式,掌握直角三角形的性质:30°所对的直角边是斜边的一半是解题的关键.

练习册系列答案
相关题目
20.下列运算中,正确的是( )
| A. | 5m-m=4 | B. | (m2)4=m8 | C. | -(m-n)=m+n | D. | m2÷m2=m |
10. 若某几何体的三视图如图,则该几何体的全面积是(平方单位)( )
若某几何体的三视图如图,则该几何体的全面积是(平方单位)( )
 若某几何体的三视图如图,则该几何体的全面积是(平方单位)( )
若某几何体的三视图如图,则该几何体的全面积是(平方单位)( )| A. | 78π | B. | 51π | C. | 36π | D. | 24π |
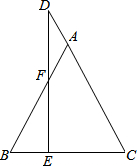 已知:如图,在△ABC中,AB=AC,D为CA延长线上一点,DE⊥BC,交线段AB于点F.请找出一组相等的线段(AB=AC除外)并加以证明.
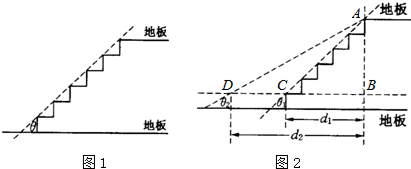
已知:如图,在△ABC中,AB=AC,D为CA延长线上一点,DE⊥BC,交线段AB于点F.请找出一组相等的线段(AB=AC除外)并加以证明.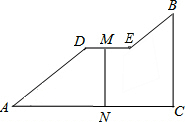 如图是一座人行天桥的引桥部分的示意图,上桥通道由两段互相平行并且与地面成36°角的楼梯AD、BE和一段水平平台DE构成.已知天桥高度BC≈4.5米,引桥水平跨度AC=7米.
如图是一座人行天桥的引桥部分的示意图,上桥通道由两段互相平行并且与地面成36°角的楼梯AD、BE和一段水平平台DE构成.已知天桥高度BC≈4.5米,引桥水平跨度AC=7米.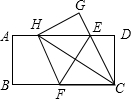 如图,在一张矩形纸片ABCD中,AB=4,BC=8,点E,F分别在AD,BC上,将纸片ABCD沿直线EF折叠,点C落在AD上的一点H处,点D落在点G处,则线段BF的取值范围为3≤BF≤4.
如图,在一张矩形纸片ABCD中,AB=4,BC=8,点E,F分别在AD,BC上,将纸片ABCD沿直线EF折叠,点C落在AD上的一点H处,点D落在点G处,则线段BF的取值范围为3≤BF≤4.